Graphing the derivative
When you have a function f(x) stored in \Y1, and you want to graph its first (and second)
derivatives, just put
...
\Y2=nDeriv(Y1,X,X) first
derivative f'(x) of f(x)
\Y3=nDeriv(Y2,X,X) second
derivative f"(x) of f(x)
Remark
On this calculator you cannot compute the third
derivative in this way. You'll get a message, ILLEGAL NEST.
The only problem is how to set the window.
Here is one way:
Assuming that you want to graph the second
derivative between the values a and b. (##)
Set Xmin=a, and Xmax=b.
From the home screen, compute
Y3(a+(b-a)rand(10))→L1 ENTER
(See the explanation for this at ** below.)
Now under WINDOW, set Ymin=min(L1), and Ymax=max(L1). Graph Y3, and adjust the window.
Example 1.
\Y1=Xsin(X)+.5X^2
\Y2=nDeriv(Y1,X,X)
\Y3=nDeriv(Y2,X,X) only Y3 is selected
a=4, b=9, (mode: radians)
Y3(4+5rand(10)) →L1
{6.495122105 4.9...
WINDOW
Xmin=4
Xmax=9
...
Ymin=min(L1)
Ymax=max(L1) this
is what you enter
...
GRAPH
(WINDOW required only a small adjustment.)
**
Explanation of the code Y3(a+(b-a)rand(10))→L1
rand(10) creates a sequence of 10 numbers
between 0 and 1;
(b-a)rand(10) transforms it into a sequence of
numbers between 0 and (b-a);
so, a + (b-a)rand(10) creates a sequence of numbers
between a +0 = a and a + (b –
a) = b, which is the domain on which we want to
graph the second derivative (marked ## above).
Example 2, from the unit Making an open box with maximal volume. Let’s graph the first derivative.
\Y1=(11-2X)(8.5-2X)X
\Y2=nDeriv(Y1,X,X) first
derivative f'(x) of f(x)
We know the domain of X: from 0 to 4.5.
We need to find a reasonable range of Y.
From the home screen, enter
Y2(0+ (4.5-0)rand(10)) →L1
You will get 10 random numbers stored in L1.
In WINDOW, set Ymin=min(L1)
Ymax=max(L1)
I prefer to put AXES ON.
Now GRAPH. (You may have both Y1 and Y2 highlighted.)
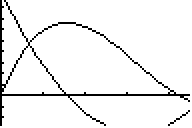
You may want to change Ymin to be smaller:
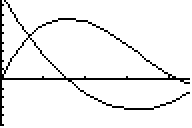
Calculus Index