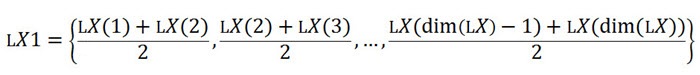Making an open box with maximal volume

This collection of boxes was made by a sixth grade class, who explored which one has the largest volume.
Task 1.
Using an 8 1/2 inch by 11 inch sheet of stiff paper (e.g., cardstock), make an open box by cutting out four squares from the corners. Compute the volume of the box. Compare the volume of your box with that of your neighbor(s). Are they the same? If not, which one has a bigger volume?
Let x be the height of the box in inches. Then:
Volume of box = length*width*height = (8 1/2 -2x)*(11-2x)*x cubic inches.
What is the biggest that x (height) can be? The height can vary between 0 and 4 1/2 inches: 0 < x <= 4 1/2 inches.
Task 2. (requires a TI-83/84 calculator)
Let's investigate the volume of the box for different heights x, and see if we can find a height for which the volume is the largest possible. We want to make a list of pairs of values for height and volume, so we will use List on the calculator. Let's use 1/4 inch increments for x, and let the width of the paper be A and the length of the paper be B. (The height is capital X on the calculator.) From the home screen, enter:
"(A-2LX)*(B-2LX)*LX"→V
The quotes are used so that, when the values of the variables are changed, the value of the expression changes accordingly. That is, quotes allow the expression to be defined dynamically.
"ΔList(LV)/ΔList(LX)"→R
R is a list of rates of change, namely, the difference of two adjacent volumes divided by the difference of two adjacent heights.
8.5→A:11→B
{.25,.5,.75,1,1.25,1.5,1.75,2.2.25}→X
You may want to go farther and instead enter
{.25,.5,.75,1,1.25,1.5,1.75,2,2.25,2.5,2.75,3,3.25,3.5,3.75,4,4.25}→X
Now in STAT Edit enter:
Name=X
Name=V
Name=R
The three lists will fill in automatically.
You can scroll down and get a few more values:
So you can see that the volume starts at 21 cubic inches (when X = 1/4 inches), up to 66 cubic inches (at X = 1.5 inches), and back down to 58.5 cubic inches (at X = 2.25 inches). So the maximum volume V shown in the table, V = 66 cubic inches, is at height X = 1.5 inches.
Notice that as the height changes from .25 to .5 inch, the volume changes from 21 cubic inches to 37.5 cubic inches.
The first rate of change R shown in the table is 66. It is computed as (37.5-21)/(.5-.25). Can you see how the remaining R values are computed? (The R in a given row refers to the heights and volumes in that row and the row just below.) Notice that R starts out big and positive, then gets smaller and negative. It crosses from positive to negative between X = 1.5 and X = 1.75 inches.
What does it mean for a rate of change to be negative?
You can change the values of X as follows:
{1.5,1.55,1.6,1.65,1.7,1.75}→X
Then look at STAT Edit:
Now you see the maximum volume V is for a height X of between 1.55 and 1.6 inches, and that is where the rate of change changes from positive to negative (i.e., where the rate of change crosses zero)!
Try it again with more finely-grained values for X:
Now we see the maximum volume is about 66.148 cubic inches, with height about 1.58 or 1.59 inches, and this is where the rate of change R is zero.
Make the box with height about 1.58 inches. You will need to change this number to one inch and some number of 16ths of an inch. (To do this, solve this equation for x: x/16 = .58. Do you see why?)
Task 3.
In Y1 enter:
\Y1=(A-2X)*(B-2X)*X
Under MATH, choose Solver. Enter:
EQUATION SOLVER
eqn:0=nDeriv(Y1,X,X)
This equation when solved will indicate for which value of X the rate of change is zero.
Press ENTER and you will see
nDeriv(Y1,X,X)=0
A=8.5
B=11
X=(put a guess here; a reasonable one is X=2)
Put the cursor in the line X= .
Now press ALPHA SOLVE.
You will see:
X=1.5854180704...
Now from the home screen,
Y1(X)
66.14823499
Compare these values for X and Y1(X) with the height and volume in Task 2.
To see the rate of change of the rate of change, you may do this:
From the home screen, enter
"seq((LX(I)+LX(I+1))/2,I,1,dim(LX)-1)"→X1
As above, the quotes allow the expression to be defined dynamically.
The expression above computes the following:
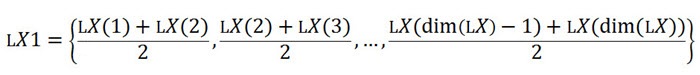
This list, LX1, contains the midpoints of LX(I) and LX(I+1), for I changing from 1 to dim(LX)-1.
So, for example, its first member is (.25 + .5)/2 = .375 = 3/8.
When you get this list, you may change the members into fractions with
→Frac
Earlier, we had the following:
height of box |
x1 |
|
x2 |
|
x3 |
|
x4 |
volume |
V1 |
|
V2 |
|
V3 |
|
V4 |
|
|
R1 |
|
R2 |
|
R3 |
To compute the rate of change of the rate of change, we need to compute R2-R1, R3-R2, ...
Again, from the home screen, enter
"ΔList(LR)/ΔList(LX1)"→R1
Using STAT Edit, enter X1 and R1.
Task 4.
Create open boxes with maximal volumes from 5*8 and 4*6 index cards by cutting out squares from each of the four corners. Show how you did it.
Task 5.
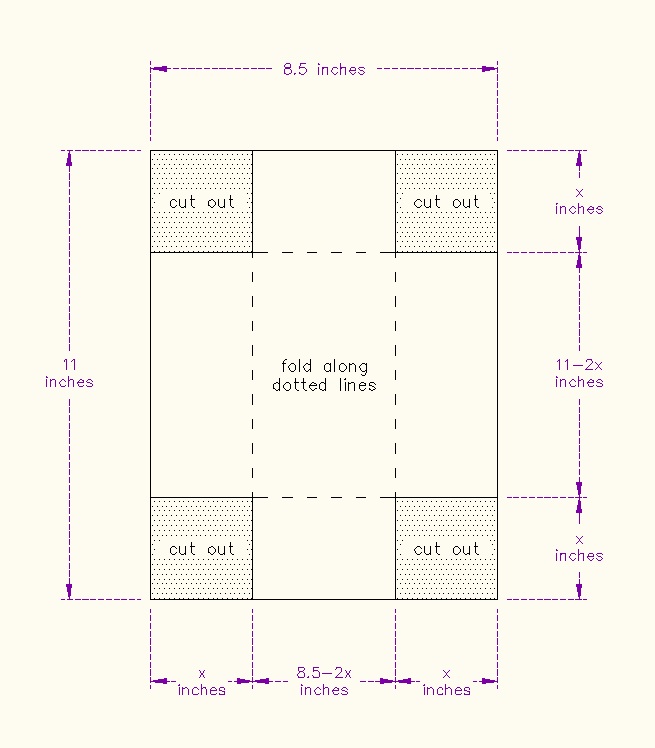
Make a box with maximal volume that will close from an 8 1/2 inch by 11 inch piece of paper.
Webpage Maintained by Owen Ramsey
Calculus Index