Rectangle in an isosceles triangle

1. Draw an isosceles triangle with base 10 cm and height 15 cm. Cut it out.

 

Using paper of a different color, design a rectangle that will fit in the triangle. A base of the rectangle should sit on the base of the triangle. Cut out the rectangle, and check that it fits in the triangle.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Find the area of your rectangle. Compare it with the areas of your neighbors' rectangles. Is it the biggest possible rectangle?

 

2. Your task is to find (and construct from paper) the biggest possible rectangle (biggest means biggest in area), and to tell how you did it. Paste it into your triangle.

 

One algebraic solution (see diagram above):

Arearectangle = x*y

Triangles ABC and ADE are similar. (Why?) So

 

 

  

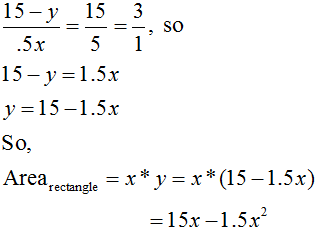
What next? Lists? Solver with nDeriv? Graphing with CALCULATE? By hand?

 

3. What percentage of the area of the triangle does the biggest rectangle cover?

Another view of a rectangle in a triangle

Webpage Maintained by Owen Ramsey
Calculus Index