Another View of a
Rectangle In a Triangle
|
Problem Find the biggest rectangle that is inscribed in an equilateral triangle and that stands on the triangle's base. "Biggest" means the biggest area. (After you solve this problem you will see that the height of the biggest rectangle is one half of the height of the triangle.) 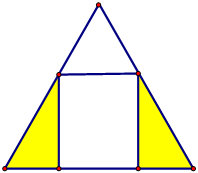 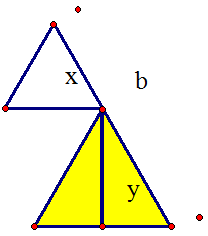 Split the side b of the triangle into two parts, x and y, so that the sum of the areas of the two small triangles, similar to the big one, built on x and y, is as small as possible. Algebraic Model Now b, x, and y will mean the lengths of the segments drawn on the side of the triangle above. The areas of the big triangle and the triangles built on x and y are C*b2, C*x2, and C*y2 where C = .25*√(3), for an equilateral triangle. (If you start with an isosceles triangle, C=sin(top angle)/2.) Remarks The value of C will be unimportant. For any similar figures, their areas are proportional to the squares of their bases. When x = y, we have x = b/2 = (x + y)/2. We will show the following algebraic theorem, which holds for all real numbers, b, x, y, and C > 0, independent of any geometric interpretation. If x + y = b then, C*x2 + C*y2 ≥ 2*C*(b/2)2 Comment Geometrically, this means that the sum of the areas is the smallest when x = y, and in turn, it means that the area of an inscribed rectangle is the biggest when its height is one half of the height of the big triangle. Proof of the Theorem 1. Simplifications Because C > 0, we may cancel it, and after substituting x + y for b, we have x2 + y2 ≥ .5*(x + y)2. This is equivalent to 2*(x2 + y2) - (x + y)2 ≥ 0. (This says that twice the sum of squares is bigger than or equal to the square of the sum of two numbers. 2. Derivation 2*(x2 + y2) - (x + y)2 = 2*x2 + 2*y2 - x2 - 2*x*y - y2 = x2 + y2 - 2*x*y = (x - y)2 ≥ 0, because it is a square. [lesson index] |