Coordinating abstract, physical, and computational aspects of algebra in a single lesson
|
NCTM
Research Presession |
|
|
Patricia Baggett |
Andrzej Ehrenfeucht |
|
Dept. of Math Sciences |
Computer Science Dept. |
|
New Mexico State
University |
University of Colorado |
|
Las Cruces, NM 88003-8001 |
Boulder, CO 80309-0430 |
|
http://www.math.nmsu.edu/~breakingaway/ |
|
Background
Our observations come from a group of math courses that are specially prepared for practicing and future teachers and taught at New Mexico State University in Las Cruces. The courses, which include algebra and calculus, are taught in a laboratory format involving hands-on applications of mathematics. Most tasks involve the design and construction of physical objects, which require specific mathematical knowledge and techniques for their completion.
General comments
We do not consider abstract algebra to be "... devoid of any meaning beyond the formal consequences of the postulates ..."
The development of "Modern Algebra" (e.g. Birkhoff & McLane) in the second quarter of the twentieth century was not based on the study of "formal axiomatic systems", but on the study of abstract mathematical structures which are "models" for such systems and which cannot be completely characterized by any system of axioms (Gödel, Skolem).
Algebra provides a language for the rest of mathematics. But the same variables, expressions and formulas can have different meanings not only in different contexts, but also at different stages of solving one problem.
Algebraic variables, expression and formulas, which are taught in schools, have three different meanings:
(a) Abstract meaning
They are descriptions of the properties of real numbers that form an abstract mathematical structure called a complete ordered field, which underlies analytic geometry, calculus, and modern probability theory. The rules of algebra are general statements about real numbers.
(b) Physical meaning
They are used to describe physical events and objects. Variables name physical attributes that can be measured, and algebraic equations express physical relationships among measured quantities. Such descriptions are called mathematical models of objects and events.
(c) Computational meaning
Algebraic expressions are algorithms that describe processes of arithmetic computations. Expressions can be used as programs that are entered into scientific calculators and executed automatically. Or they can provide descriptions of the order in which arithmetic operations should be carried out on paper.
Here is an example of a solution to a problem in which algebra is used in all three of the ways described above.
Problem
An isosceles triangle, with its height equal to its base, was circumscribed around a circle with a given radius r (Picture 1). Express the area A of the triangle as a function of r. And describe how you would compute it on the TI-34 II calculator.
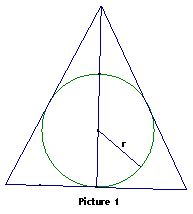
Solution
Part 1. Constructing a math model of the situation
Declaration of variables
r radius of the circle (given);
h height of the circumscribed triangle (unknown);
b the length of the triangle's base (unknown);
A the area of the triangle (to be computed);
s, t the lengths of the two sides of the triangle coming up from the base
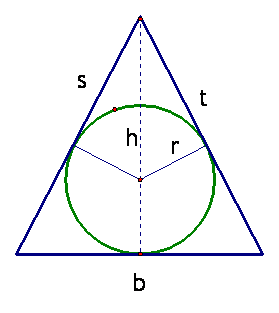
Relations among the variables
(1) h = b stated in the problem;
Part 2. Derivation of formulas
(1) s = t = √(5)/2*h Pythagorean theorem;
(2) s + t + b = s + t + h perimeter of triangle
= √(5)/2*h + √(5)/2*h + h
= √(5)*h + h = h(√(5) + 1)
(4) Also, A =
b*h/2 = h2/2 = ½
(perimeter of triangle)*r.
Why is this so?
The triangle can be divided into three triangles, each with height r and each
with a base equal to one side of the triangle:
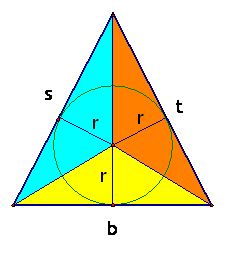
So A = ½*r*s +
½*r*t + ½*r*b =½*r*(s+t+b)= ½*r*perimeter of triangle.
Thus A = ½ h(√(5) +
1)*r
So canceling h/2, we have h = (√(5) + 1)*r
Thus A = h2/2 = (√(5)
+ 1)2*r2/2
This formula
shows A as a function of r.
Part 3. Program for the TI-34 II
Enter,
OP1=(√(5)+1)2/2*Ans2
To use it, enter the value of r and then press OP1. The value of A is displayed.
Comments
In part 1, the variables represent lengths of different segments, with the exception of A, which is the area of the triangle; and the formulas describe the relationships among them. In this part students construct a mathematical model of the situation (meaning (b)).
In part 2, the variables range over abstract numbers. The derivation of formulas is independent of their physical interpretation with only one exception.
The equation, 5r2 = (h - r)2, is equivalent to the following alternative,
Either √(5)r = h - r or -√(5)r = h - r.
But we consider only, √(5)r = h - r, because the geometric quantities involved can have only positive values. In algebraic derivations, meaning (a) is used. Any physical meaning of the variables is irrelevant.
In part 3 the expression for A becomes a program for the TI-34 II calculator. The only change is a replacement of variable r by Ans, which is the name of a location in the calculator's memory holding the number displayed on the screen. An algebraic expression is a program (meaning (c)).
The example above is an illustration of how the meaning of algebraic entities may change during the solution of one problem. But this example doesn't provide a viable lesson plan. As a lesson plan it has three fatal errors.
First, a quite feasible physical event is presented as a "story problem". Most students do not have enough experience with practical geometric constructions to see it as a problem about a circle and a triangle drawn on paper.
The second fatal error is that the students do not carry out the actual computation, so they do not "see" the execution of an algebraic expression used as a program and the answer it produces.
Finally they do not have any practical way to check if their solutions are correct. They must rely on a teacher's evaluation of their work. So their goal is not a correct answer but a teacher's approval of it.
To change this example into a lesson plan is not hard. First, you may ask students to draw a circle with a compass, and then circumscribe around it an isosceles triangle with its base and height equal. (This construction can be done without making any measurements; we present it in the seven steps below.)
1. Using a compass, draw a circle with radius r. Draw a vertical diameter (dotted below). Label the point where the diameter touches the circumference at the top C.
2. Construct a segment perpendicular to the diameter, tangent to the circle at the bottom. Label the tangent point P.
3. Put the point of the compass at tangent point P and swing 2 arcs one radius away to cut the tangent line in two places. Label them A and B.
4. Construct triangle ABC. It is isosceles, and its height equals its base.
We will construct a triangle similar to ABC but circumscribed around the circle.
5. Using an index card, construct two segments, perpendicular to AC and to BC, through the center of the circle. Extend the segments to the circumference of the circle. Label where the segments cut the circle D and E.
6. Extend segment AB.
7. Draw segments parallel to AC and BC through D and through E. They cut AB at F and G, and call where they intersect H.
The desired triangle is FGH. It is isosceles, and its height equals its base.
And we didn't do any measuring!

***
After they finish the task described in the example shown above, they can measure the radius of their circle, and the height and the base of their triangle. Then they can compute the value of A in two different ways: As a function of r using the program OP1, and as A = b*h/2 using the values of b and h that they have measured. When the difference between these two answers is too big to be attributed to rounding errors (while measuring), students know that the solution they propose is not correct.
Closing remarks
We interpret "... the conceptual independence of mathematical structure from empirical contexts of application ..." as a (correct) claim that the three interpretations (a), (b), and (c) of the language of algebra can be taught independently of each other. Interpretation (a) can be seen in a course of abstract algebra for math majors; (b) fits an introductory course in experimental physics; and (c) has been used in programming courses at the time when numerical programs played a central role in computer science curricula.
We think that teaching algebra while ignoring differences between the abstract concept of real numbers and the concrete quality of measurements of physical attributes (for example, by teaching algebraic equalities as a process of balancing groups of objects on scales) simultaneously misrepresents both interpretations.
In order to be able to solve practical problems, students need to create a mathematical model of a situation (this requires (b)), carry out appropriate algebraic derivations (this requires (a)), and plan and execute numerical computation (this requires (c)). In this context, the three meanings, abstract, physical, and computational, are not independent any longer. For example:
The equations representing relationships among physical quantities are used as assumptions in the derivation of other formulas.
The expression representing A as a function of r, which is the result of a rule-based derivation, is used as a program. And the result of computation is interpreted as the area of a triangle within the mathematical model of the original task.
High school teachers who take our courses usually have more than adequate skill and understanding of abstract algebra to do the hands-on projects. But they struggle with constructing mathematical models of concrete situations because it was never a part of the algebra and calculus courses they took before. The "applications" used in such courses have consisted only of word problems with "practical" content. Similarly, teachers' skills in planning computations strongly depend on their previous experiences with computers and calculators.
We have never observed any specific transfer of skills or understanding among the three interpretations of algebra we have discussed. But our experience shows that they can be taught simultaneously within one course.
References
Birkhoff G. & S. McLane (1953). A
Survey of Modern Algebra, revised edition (
Kurt Gödel http://en.wikipedia.org/wiki/G%C3%B6del
Upwards Skolem-Löwenheim theorem http://everything2.com/index.pl?node_id=545232&lastnode_id=0
Webpage developed by Aous Manshad
Last Modified: October 13, 2019