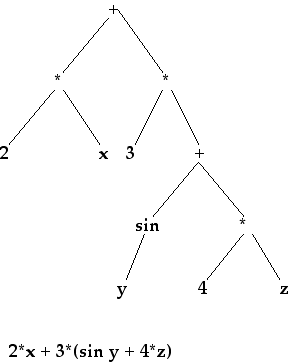
El Lenguaje del álgebra
<< Volver al índice y Calidad ...
Todos los campos de las matemáticas modernas usan fórmulas y expresiones algebráicas. Por ello, la anotación algebráica se ha universalizado grándemente, a pesar de que los significados de las expresiones y fórmulas pueden ser muy distintos en diversos campos matemáticos. Tales diferenciaciones pueden crear confusión, y especiálmente porque los matemáticos son un tanto parsimoniosos en su elección de los símbolos. Incluso los símbolos más comunes en matemáticas, tales como +, -, >, y =, se usan con cierta liberalidad en otros campos de las matemáticas, teniendo éstos significados muy distintos de sus significados aritméticos originales.
Así, con frecuencia decimos que el álgebra provee de un lenguaje para todas las matemáticas. Pero el uso de tal lenguaje se halla fuértemente regulado por sus reglas gramaticales, las cuales describen cómo palabras y frases individuales se relacionan entre sí, y cómo éstas forman frases y textos coherentes. ¿Tiene el álgebra, como lenguaje que es, una gramática? ¿Cuáles son sus palabras y cómo se relacionan entre sí?
Revisaremos aquí sólo las expresiones algebráicas que son comunes a la parte del álgebra que se enseña en las escuelas antes de enseñar el concepto general de función, y también antes de que se introduzcan anotaciones de funciones, tales como f(x), g(g), etc.
Los bloques constructivos básicos que juegan el papel de palabras en álgreba son:
? números, los cuales se escriben usuálmente en forma decimal;
? variables y constantes, tales como x, y, área, altura, z1, z2,
c, π y demás; y
? símbolos especiales para operaciones y funciones, tales como +, *, -, sen,
cos, √?, etc.
Los números y las variables tienen expresión en sí mismos, pero las operaciones y las funciones necesitan de algunas entradas para poder producir valores. Algunas de ellas (p.e., +, *, y -) requieren dos entradas, mientras otras (p.e., sen, cos, y √? ) requieren sólo una entrada.
Las reglas gramaticales del álgebra gobiernan qué valores se introducen en qué operaciones. Cuando se usan expresiones algebráicas en diferentes dominios matemáticos, los significados de las variables y otros símbolos pueden cambiar, si bien las reglas gramaticales permanecen constantes. Esto es más que una simple conveniencia. Muchos problemas en matemáticas pueden resolverse sin mirar al significado, tan sólo mirando a las reglas. Esta parte de las matemáticas se ha dado en llamar ?simbólica? o ?formal,? si bien ahora con frecuencia se la conoce como ?algorítmica?. Esta característica de las matemáticas ha permitido la moderna automatización del procesamiento de datos. Los ordenadores nunca procesan significado en un sentido humano. Antes bien, éstos procesan datos, usando sólo características "formales" de dichos datos.
Cabe advertir aquí que, de igual modo que diferentes lenguajes humanos tienen diferentes gramáticas, así también la gramática del álgebra escolar no es la única posible. No sólo son posibles otros lenguajes de álgebra, sino que además ellos son comúnmente utilizados en los procesos realizados por los ordenadores.
Un correcto conocimiento de la gramática algebráica es una condición necesaria para poder entenderla. Es aún más importante que un conocimiento adecuado de la gramática de los lenguajes humanos. Cuando hablamos, la mayor parte de la información es transmitida con las palabras. Además, nuestro conocimiento mundano nos permite entender textos incluso si aquellos tienen algún fallo. En álgebra, como en matemáticas en general, la parte más importante de la información yace no sólo en los números, las variables y las operaciones, sino en la relación entre todos éstos. Así, errores gramaticales siempre conducen a errores conceptuales. Pero lo que uno obtiene con el aprendizaje de la gramática es muy substancial, ya que nos provee con la base suficiente para gran parte del procesamiento algebráico. Afortunádamente la gramática algebráica es fácil; más fácil que las gramáticas de los lenguajes humanos.
Notas.
Existe una tendencia en la educación matemática a postponer las matemáticas "formales" hasta que los estudiantes aprenden los tópicos a un nivel intuitivo. El retrasar la introducción de matemáticas formales es al menos parciálmente posible en aritmética y geometría, porque todos tenemos una noción intuitiva de los conceptos de cantidad y espacio. Pero el álgebra es, predominántemente, un lenguaje, y la única forma de poder dominar un lenguaje es a través de aprender a usarlo.
Se puede también cuestionar la supuesta sabiduría en el postponer el uso de anotaciones algebráicas hasta la escuela media puede también cuestionarse. No existe una edad mínima para que los niños/as puedan empezar a aprender su segundo idioma. Por lo tanto, resulta difícil explicar por qué el álgebra debería ser una excepción. Un posible argumento a favor de la postposición, basado en que el álgebra es sólo un lenguaje escrito, se debe a una desafortunada tradición en la enseñanza. La habilidad necesaria para la lectura correcta de fórmulas algebráicas, imbuyéndolas en el español informal (o el inglés,...) no se enseñan en ningún nivel. Comenzando el álgebra tan pronto como la aritmética requeriría un alejamiento de esta desafortunada tradición.
La estructura de las expresiones algebráicas.
Cada expression algebráica (y matemática) posee una estructura estrictamente jerarquizada, lo que en matemáticas se denomina un árbol (dibujado al revés). En su parte inferior se hallan los números variables, los cuales forman las hojas del árbol. Sus valores son introducidos a las funciones (operaciones), las cuales proveen de valores a otras funciones, hasta que se alcanza un valor final. (Ver el diagrama.)
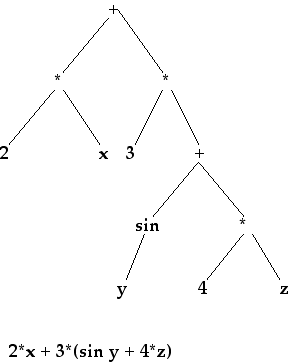
2 y x son las entradas para la primera multiplicación,
4 y z son las entradas para la última multiplicación, mientras que y es
la entrada para la función del seno.
El seno y la última multiplicación proveen la entrada para la segunda suma, la
que junto a 3, provee la entrada para la multiplicación intermedia. Las
multiplicaciones primera e intermedia proveen a su vez de las entradas para la
suma de la parte superior, la cual arroja el valor final de la fórmula.
Note que no necesitamos saber los valores de x, y ó z, ni tampoco cómo se desarrollan las operaciones, ni cuál es la función del seno, para poder entender cómo todas estas "piezas" se interrelacionan.
La expression algebráica usual para este árbol es:
2*x + 3*(sen y + 4*z)
Conocer la gramática algebráica es saber cómo se construye un árbol para una expresión algebráica dada. Para escribir un árbol uno ha de saber que la prioridad de las operaciones coloca al seno en la parte superior, antes de la multiplicación, la cual está más arriba que la suma, y que el paréntesis tiene prioridad sobre todas las operaciones.
Esto se puede leer como, "2 multiplicado por x más 3 veces el seno de y, más 4 veces z." Tal lectura es ambigua porque no muestra el paréntesis. Se puede indicar el paréntesis mediante anotación, pero al dictarlo es mejor leer "2 multiplicado por x, más 3 multiplicado, abrir paréntesis, seno de y más 4 veces z, cerrar paréntesis."
Existen lecturas alternativas que a veces son menos ambiguas, tales como "2 multiplicado por x, más 3 multiplicado por la suma del seno de y, más 4 veces z." No obstante, no hay una manera segura de evitar la ambigüedad en la lectura de expresiones algebráicas, sin mencionar los paréntesis.