Knowing an Ellipse

---

A simple mathematical model of an ellipse consists of parametric equations,

X = Lcos(T)

Y = Ssin(T)

where T is an angle measured in radians, 0 ≤ T ≤ 2π, and L and S are half-lengths of the long and short axes of the ellipse.

Its area A and the perimeter P are

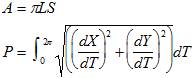
The derivatives of X and Y relative to T are

dX/dT = -Lsin(T)

dY/dT = Scos(T)

Therefore,

Programs
Define in parametric mode,
\X1T=Lcos(T)
\Y1T =Scos(T)

Define in function mode,
\Y1= fnInt(√(L²sin(T)² + S²cos(T)²),T,0,2π)

From the home screen, in parametric mode, enter the values of L and S; set the window to ZStandard, Zsquare; GRAPH; you will see an ellipse,

CLEAR; and compute the area A and perimeter P of the ellipse, rounding them reasonably.

Example

7.5→L:5.5→S	ENTER
	5.5
round(πLS,0)→<A/td>	ENTER	GRAPH	(look carefully at the picture of your ellipse)
	130	CLEAR
round(Y1)→P	ENTER
	41.1

Repeat this several times to become familiar with the shapes, sizes, perimeters, and areas of ellipses.

Draw one ellipse (which you have displayed on your calculator) on paper, taking one centimeter as a unit and drawing the x- and y-axes. (It is best to use graph paper for this task!)

In order to get points (x, y), which you will connect to draw the ellipse, use 2nd TBLSET, and enter TblStart=L, ΔTbl=1

Then get the values x and y from 2nd TABLE, where you will see T, X1T, and Y1T, which you can scan using up and down arrows.

---

Webpage Maintained by Owen Ramsey
Calculus Index