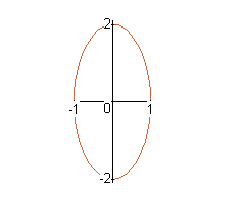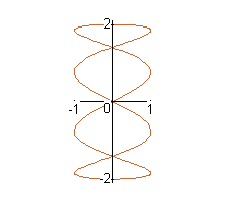Cool websites and information for
figures drawn from parametric equations (Lissajous
figures)
From
http://www.math.com/students/wonders/lissajous/lissajous.html
Lissajous (pronounced LEE-suh-zhoo) figures were discovered by the French physicist
Jules Antoine Lissajous. He would use sounds of
different frequencies to vibrate a mirror. A beam of light reflected from the
mirror would trace patterns which depended on the frequencies of the sounds. Lissajous' setup was similar to the apparatus which is used
today to project laser light shows.
Before the days of digital
frequency meters and phase-locked loops, Lissajous
figures were used to determine the frequencies of sounds or radio signals. A
signal of known frequency was applied to the horizontal axis of an
oscilloscope, and the signal to be measured was applied to the vertical axis.
The resulting pattern was a function of the ratio of the two frequencies.
Lissajous figures often appeared as props in science
fiction movies made during the 1950's. One of the best examples can be found in
the opening sequence of The Outer Limits TV series. ("Do not
attempt to adjust your picture--we are controlling the
transmission.") The pattern of criss-cross lines is actually a Lissajous figure.
From
http://mathworld.wolfram.com/LissajousCurve.html
From
http://www.abc.net.au/science/holo/liss.htm
Jules Antoine Lissajous
was a French physicist who lived from 1822 to 1880. Like many physicists of his
time, Lissajous was interested in being able to see
vibrations. He started off standing tuning forks in water and watching the
ripple patterns, but his most famous experiments involved tuning forks and
mirrors. For example, by attaching a mirror to a tuning fork and shining a
light onto it, Lissajous was able to observe, via
another couple of mirrors, the reflected light twisting and turning on the
screen in time to the vibrations of the tuning fork. When he set up two tuning
forks at right angles, with one vibrating at twice the frequency of the other, Lissajous found that the curved lines on the screen would
combine to make a figure of eight pattern.
From
http://www.math.ucla.edu/~ronmiech/Calculus_Problems/32A/chap9/section1/553d39/553_39.html
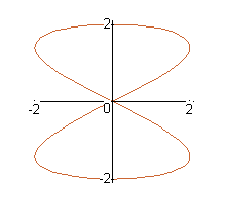
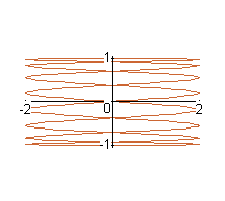
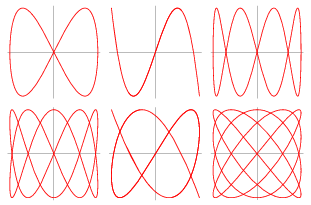
The curves with equations x=a*sin(nt), y = b*cos(t) are called Lissajous figures. Investigate how these curves vary when a, b and n vary. (Take n to be a positive integer.)
Solution:
|
a = 1, b = 1, n= 1
|
a = 1, b = 2, n=1
|
a = 2, b = 2, n=2
|
|
a = 1, b=2, n = 4
|
a = 2, b = 2, n = 4
|
a = 2, b= 1, n = 8
|
Calculus Index