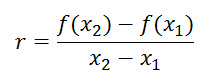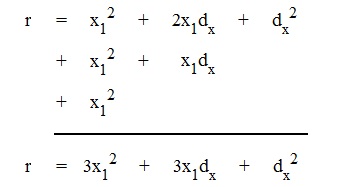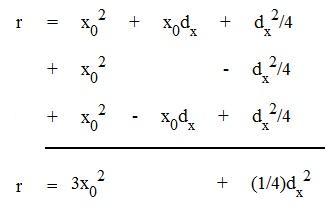Rate of Change and Derivative 2

---

Let variable y be a function of variable x. We often write it as y = f(x). The rate of change r of variable y relative to variable x, when x changes from x₁ to x₂, is

It is the ratio of the change of y to the change of x.

Generic example
In this example we will use f(x) = x³.
Variables

x	x is the independent variable
y = f(x) = x^3
y1 = f(x1)
y2 = f(x2)
dx = x2 - x1	change of x from x1 to x2
dy = y2 - y1	change of y from y1 to y2
r = dy/dx = (f(x2) - f(x1))/(x2 - x1)	(Here dx must be different from 0, dx ≠ 0.)

Examples of the rate of change r

x1	x2	y1	y2	dx = x2 - x1	dy = y2 - y1	r = dy/dx
0	2	0	8	2	8	4
.5	1.5	.125	3.375	1	3.25	3.25
0.9	1.1	.729	1.331	.2	.602	3.01

Algebraic computation of r

r = (f(x₂) - f(x₁))/(x₂ - x₁)

(x₂³ - x₁³)/(x₂ - x₁).

But x₂ - x₁ = d_x

and x₂³ - x₁³ = (x₂² + x₂x₁ + x₁²) * (x₂ - x₁),

because a³ - b³ = (a² + ab + b² )*(a - b). (You may check this yourself!)

So

r = x2^2 + x2x1 + x1^2,

(i)

because x₂ - x₁ = d_x ≠ 0; and since it is in the numerator and denominator of r, it can be canceled.

Now in (i) above we substitute x₁ + d_x for x₂.

r

=

(x1 + dx)^2 + (x1 + dx)x1 + x1^2, so

We see that r depends on both the initial x₁ and the amount of change, d_x. The original formula for r had no value for d_x = 0, because you cannot divide by 0. But our new formula, r = 3x₁² + 3x₁d_x + d_x², has values for all d_x, including d_x = 0. The value of r for d_x = 0, is 3x₁², and this is called the value of the derivative of f(x) = x³ for x = x₁. (ii)

The derivative of a function f(x) is often written as f'(x) and read "f prime of x". (In our example, f '(x) = 3x².) So the derivative of f(x), for x = x₁, can be written as f '(x₁).

Now we will get a closer look at the relationship between the rate of change r of variable y = f(x) relative to x, when x changes from x₁ to x₂, and the derivative f '(x) of a function f(x).

Let's introduce one more variable, x₀.

	x0 = (x1 + x2)/2	x0 is half way between x1 and x2;
So,		x1 = x0 - dx/2, and x2 = x0 + dx/2.

But	r	=	x2^2 + x2x1 + x1^2 (see (i) above).
So we have
	r	=	(x0 + dx/2)^2 + (x0 + dx/2)( x0 - dx/2) + (x0 - dx/2)^2

But 3x₀² is the value f '(x₀) of the derivative of the function f(x) = x³, for x = x₀ (see (ii) above).

Examples of values of the derivative and the rate of change r for x₀ = 2 and 3.

x0	dx	f'(x0) = 3x0^2	r = 3x0^2 + (1/4)dx^2
2	.1	12	12.0025
2	.01	12	12.000025
3	.01	27	27.000025
3	.001	27	27.00000025

When d_x is close to 0, then the rate of change r and f '(x₀) are almost equal. This is true in general, and not just for this example. Also, x₀ doesn't have to be exactly in the middle between x₁ and x₂.

You may wonder if the r in the example just above (call it r₂) is the same as the r in the first example above (call it r₁). It is! Here is the proof that r₁ = r₂:

From above, we know x₁ = x₀ - d_x/2
and r₁ = 3x₁² + 3x₁d_x + d_x² (iii)
and r₂ = 3x₀² + (1/4)d_x²
We substitute x₀ - d_x/2 for x₁ in (iii):
r₁ = 3(x₀ - d_x/2)² + 3(x₀ - d_x/2) d_x + d_x²
r₁ = 3(x₀² - x₀d_x + d_x²/4) + 3x₀d_x - 3/2 d_x² + d_x²
r₁ = 3x₀² - 3x₀ d_x + 3/4*d_x² + 3x₀d_x - 3/2 d_x² + d_x²
r₁ = 3x₀² + 3/4*d_x² + -3/2 d_x² +d_x²
r₁ = 3x₀² + 1 3/4*d_x² + -3/2 d_x²
r₁ = 3x₀² +(1/4)*d_x² = r₂

General statement
The rate of change of f(x) when x changes from x₁ to x₀, and the value of the derivative f '(x₀), where x₀ is between x₁ and x₂, are very close to each other when dx = x₂ - x₁ is close to 0.

Remark
nDeriv, which is used by the TI-83/84 calculator, computes the numerical value of f '(x₀) by computing r for a small d_x. For details see the manual.

Final remarks
1. The mathematical concept of a derivative captures the intuitive concept of the instantaneous rate of change that is used in physics. Its introduction marked the creation of calculus and started the mathematical foundations of modern science. It was first used to describe instant velocity (velocity at a given moment) and instant acceleration, which is the rate at which velocity changes at a given moment. One of the basic equations of physics, discovered by Newton, states that the acceleration a of an object is always proportional to the sum of all forces F acting on the object, a = F/m, where the constant m is its mass.

2. When we talk about the velocity of an object, we take into consideration not only its speed, but also the direction it is moving in space.

---

Webpage Maintained by Owen Ramsey
Calculus Index