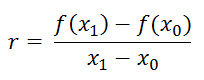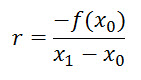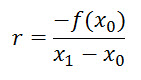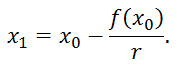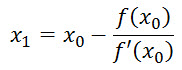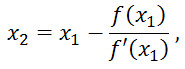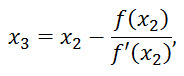More about Newton's Method

Newton's method finds an approximate solution to the equation f(x) = 0, using the concept of the rate of change.

The rate of change r of the values of the function f(x), relative to the variable x, when x changes from x₀ to x₁, is

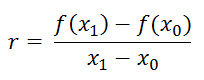
This rate of change r can be used to look for a value x₁ such that f(x₁) = 0, by solving for x₁ the equation

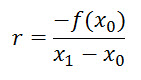
We set f(x₁) = 0, so

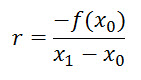
We solve this equation for x₁:

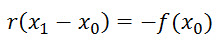
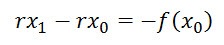
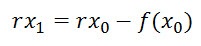
So the solution is

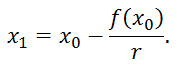
We can compute f(x₀) for any chosen x₀; but how to find r?
When the difference x₁ - x₀ is rather small (close to 0), then r can be estimated by the value of the derivative of f(x) for x = x₀.

r is approximately equal to f'(x₀)

This gives us a formula, which we can compute, that returns an approximate value of the solution of our equation, f(x) = 0:

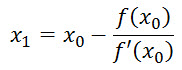
How good this approximation is depends on our choice of x₀. But the nice thing is that when we get a good approximation once, we can improve it by iterating the whole process,

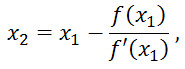
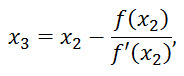
and so on.