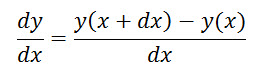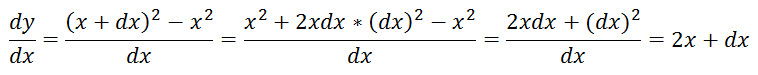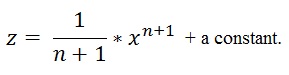Derivatives and Antiderivatives of Polynomials
1. Students should
be shown how to use Pascal's triangle to compute (a + b)n (For example, see the unit titled Pascal's
triangle: Binomial coefficients in Breaking
Away from the Algebra and Geometry Book.)
2. They should use it to compute dy/dx, for y = x, x2, x3,
and x4, using the formula
and getting the
following table:
|
|
|
|
y |
|
|
|
dy/dx |
|
|
|
|
x
|
|
|
|
1
|
|
|
|
|
x2
|
|
|
|
2*x
+ dx |
|
|
|
|
x3
|
|
|
|
3*x2
+ 3*x*dx + (dx)2 |
|
|
|
|
x4
|
|
|
|
4*x3
+ 6*x2*dx2 + (dx)3 |
(This is an exercise in algebra.)
For example, let y = x2. Then
(This is the second
entry in the above table.)
3. They should now create a list L1 of values closer and closer to 0 (with the last value 0),
for example {1, .01, -.001, .0001, -.00001, 0} and compute,
|
|
|
|
dy/dx
|
|
|
|
|
2*X
+ L1 |
|
|
|
|
3*X2
+ 3*X*L1 + L12 |
|
|
|
|
4*X3
+ 6*X2*L12 + L13 |
for several values
of x, using the TI-83/84 calculator, to see the convergence to,
|
|
|
|
2*X
|
|
|
|
|
3*X2
|
|
|
|
|
4*X3
|
4. At this point they may accept (without further proof) that when y = xn
then its derivative is (in the limit) dy/dx = n*xn-1.
5. A conclusion that the derivative of a polynomial,
|
|
|
|
y
= a*xn + b*x(n-1) + ..., is |
|
|
|
|
dy/dx
= a*n*x(n-1) + b*(n-1)*x(n-2) + ... |
follows from the
property of common fractions. If
|
|
|
|
dy
= a*dy1 + b*dy2 + ..., then |
|
|
|
|
dy/dx
= a*(dy1/dx) + b*(dy2/dx) + ... |
6. The anti-derivative of y is any z such that dz/dx = y. So
students can (algebraically) compute that,
then
(The rate of change
of a constant is 0.)
7. Applications.
(a) When computing derivatives of
polynomials it is as easy to use the "algebraic" formula as to use
nDeriv.
(b) Using antiderivatives for computing
integrals (the Fundamental Theorem) is both more efficient and more accurate
than using fnInt. (Also using antiderivatives avoids the "nesting" of
fnInt, which is not allowed on the TI-83/84.)
Calculus Index