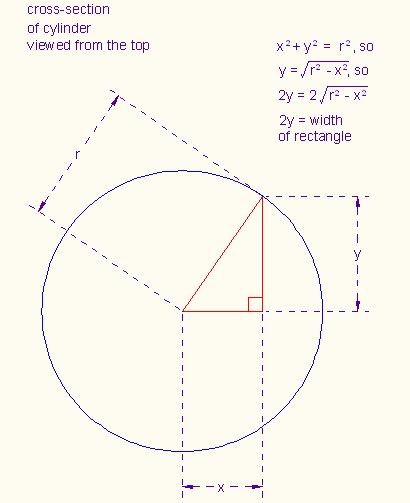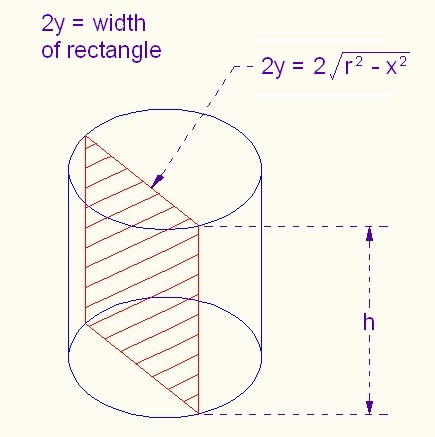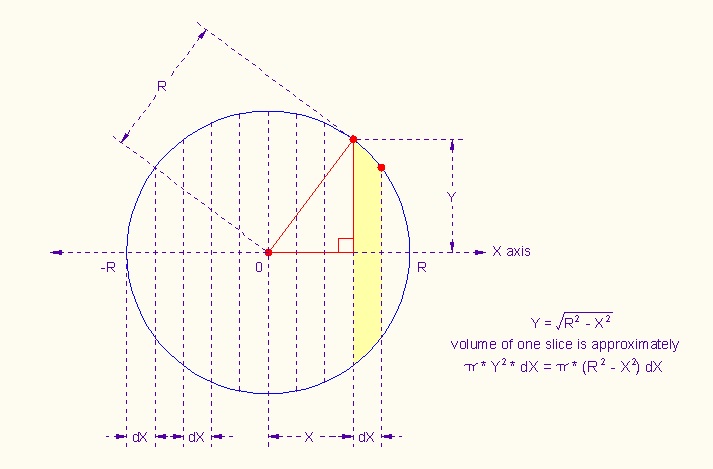
| V = 4/3πR3 . |

| π(R2 - X2)dX |
| -R∫Rπ(R2 - X2)dX |
| V = -R∫Rπ(R2 - X2)dX |
| fnInt(π(R2-X2),X,-R,R) | ENTER |
| V = 4/3πR3 and | |
| fnInt(π(R2-X2),X,-R,R) |
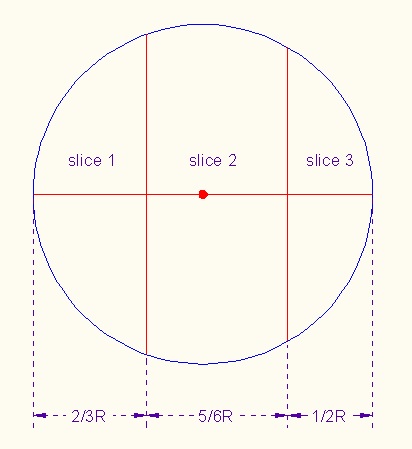
| 7→R | ENTER | ||||
| fnInt(π(R2-X2),X,-R,-1/3R) | ENTER | ||||
| fnInt(π(R2-X2),X,-1/3R,1/2R) | ENTER | ||||
| fnInt(π(R2-X2),X,1/2R,R) | ENTER |
| The second task can also be solved by an algebraic formula. And the Fundamental Theorem of Calculus (which we will discuss later) can be used to find it (using antiderivatives). But it is not a topic of this lesson. | |
| The calculator does not compute the integral directly by the method described above. It uses a very ingenious "short cut" that was invented by Gauss and later improved even more. |
| V = πR2H | |
| The other formula is, | |
| V = 0∫HπR2dX |