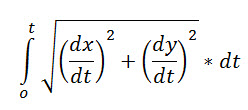Finding the circumference of a circle (and the lengths of
other curves) using calculus
Suppose you have
parametric equations for a curve:
x is a function of t
y is another function of t
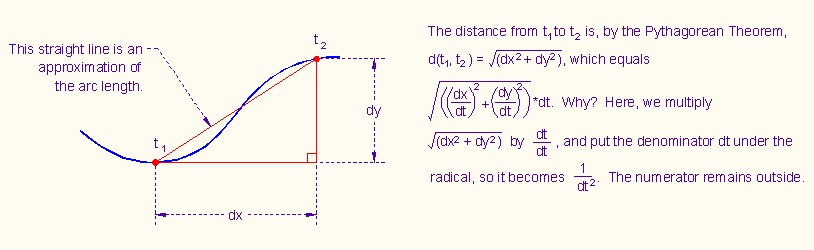
Then the arc length of the curve, when t changes from 0 to x, is given by:
Why?
Set MODE to Degree.
While in parametric mode, place the parametric equations x(t) and y(t) for the
curve under consideration in the TI-83/84 calculator. For a circle
with radius 1, these are:
\X1T=cos(T)
\Y1T =sin(T)
Next set MODE to Func, and set Y1 as the integral above, namely:
\Y1=fnInt(√(nDeriv(X1T,T,T)2 + nDeriv(Y1T,T,T)2),T,0,X)
To find the circumference, on the homescreen, enter
Y1(360)
You will see
6.283185307
How close is this to 2π?
Ans - 2π
Display: -2.68E-10
You may set MODE to Radian, and then from the homescreen, enter
Y1(2π)
Display: 6.28318426
How close is this to 2π?
Ans - 2π
Display: -1.047211E-6
To find the lengths of other curves, you do not need to change Y1! You only change
the parametric equations.
Suppose we want to find the length of the parabolic curve y = x2
from 0 to 1. It is easy. First we parameterize y=x2. A
simple way is to set x = t and y = t2.
With MODE set to parametric, enter
|
\X1T =T |
|
\Y1T =T2 |
|
Now set MODE to Func, and from the home screen, enter
|
|
Y1(1) |
|
display: 1.478942858. This is the length of the
parabolic curve y = x2 from 0 to 1! |
What is the length of the line y = x, from x = 0 to x = 1?
|
\X1T =T |
|
\Y1T =T |
|
Display: 1.414213562 |
|
Ans - √2 |
|
Display: 0 |
What
is the ratio of the length of the parabolic curve to the length of the straight
line, from x = 0 to x = 1? 1.045770524. (You can graph these on the
TI-83/84.)
The length of the parabolic
curve is only about 4.5% longer than the straight line!
Calculus Index