Elliptic Cylinder

Task.
You will be given a strip of rectangular poster board having length L and width W, and an index card. You should use the poster board to make the side wall (lateral surface) of a elliptic cylinder that has a ratio of its axes 2 to 1. Its (elliptic) base will be made from the index card. L is going to be the perimeter of the base of the cylinder, and W will be its height.

After you plan the design, I'll give you the materials so you can measure W and L, and then do the computation and make the cylinder. You can make a lid for it if you want. The last thing you are going to do is to compute the volume of the cylinder and also measure the volume using rice.

Plan.
Let S be the (unknown) length of the shorter axis of the base of the ellipse, and let L be its (given) perimeter. We will compute the perimeter P of an ellipse with axes 1 and 2. By similarity of two ellipses, the ratio S/1 = L/P, and therefore S = L/P.

Using

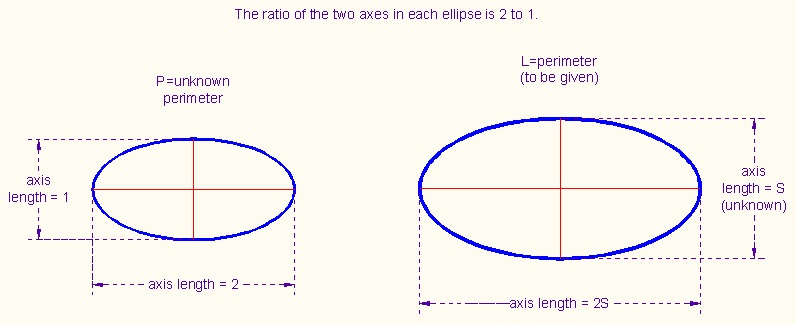
\X1T=Acos(T)

\Y1T=Bsin(T)

and running,

1→A:.5→B				ENTER				A and B are half-axes of the left ellipse above;
fnInt(√(nDeriv(
X1T,T,T)2+nDeriv(
Y1T,T,T)2),T,0,2
π)				ENTER
Ans→P				ENTER

we get ,

P = 4.8442223304 (before rounding). This is the perimeter of the ellipse with axes 1 and 2.

Now we are ready for the next step.

We measure L and W, and store the values in variables L and W.
Now we compute

L/P→S
S/2→B				ENTER				1/2 of the shorter axis of the ellipse we will draw;
2B→A				ENTER				1/2 of the longer axis;
WABπ→V				ENTER				Volume of the cylinder=area of base*height (The area of an
								ellipse with half axes A and B is πAB. Compare to the area of
								a circle, π*r*r.)

Finally we create lists LX1T and LY1T (these are the x and y coordinates of the points on the perimeter of our ellipse). One way to do this:
Set mode to Degree.
Create a sequence of T-values for 1/4 of your ellipse (from 0 to 90°) and store it in L1:

seq(T,T,0,90,5)→L1

(seq is under LIST OPS 5)

Now get X1T and Y1T values for each angle in 5-degree increments:

X1T(L1)→X

Y1T(L1)→Y

Now go to Y= in parametric mode, and highlight

\X1T=Acos(T)

\Y1T=Bsin(T)

When L=35.5 cm, we get A = 7.3283... and B=3.664...
Now go to TBLSET and set TblStart=0 and ΔTbl=5.
Next go to TABLE and you will see

X1T and Y1T are the coordinates of the points for 1/4 of your ellipse. Because of symmetry, they are all you need.

Now draw the points on cm graph paper, trace it onto posterboard (you may use the point of your compass to punch the points onto the posterboard), make two ellipses if you want a lid (see the picture above)!, cut it out, make the cylinder, and measure its volume.

You can also plot the points as follows:
Set WINDOW to Tmin=0, Tmax=90,Tstep=.5, Xmin=0, Xmax=7.5, Ymin=0, Ymax=5.
Now in STAT PLOT turn Plot1 on, and make Xlist X and Ylist Y, using the first mark.
Graph, and with X1T and Y1T highlighted, you get

---

Webpage Maintained by Owen Ramsey
Calculus Index