Circle and Ellipse

Task.
Draw a circle with radius of your choice, and draw an ellipse with the same area and a perimeter 10% longer than the perimeter of the circle. (Do you see that you cannot draw a non-circular ellipse with the same area and the same perimeter as the circle?)

Solution.
Students need to know that:
(1) The equations, x = c*cos(t), and y = d*sin(t), where t changes from 0 to 2π, describe an ellipse with axes having lengths 2c and 2d.
The area of such an ellipse is A = π*c*d.
Its perimeter p is:

For a circle with radius r, its area A = πr², and its perimeter p = 2πr. So we need to find an ellipse with area A = πcd = πr², and perimeter p = 1.1*2πr = 2.2πr.
From the equation for the area of an ellipse we know that
(2) d = r²/c.
So putting together (1) and (2), we conclude that in order to find c and d, for the required ellipse we need to solve for c the following equation,

We can speed up the process of computation if we compare 1/4 of the perimeters, because it is faster to compute an integral for a smaller range of t. So we have,

Program for the TI-84.
(In this example, in order to be concrete, we use r = 10 cm. You may choose your own r.)
With our calculator in parametric mode, we enter
\X1T=C*cos(T)
\Y1T=R²/C*sin(T)

Now place the calculator in Func mode.
Enter
\Y1=fnInt(√(nDeriv(X1T,T,T)² + nDeriv(Y1T,T,T)²),T,0,π/2)

Use Solver to enter the equation, eqn:0=Y1-.55πR, the value of R, and to initialize T to zero, and C to some value, say 3. You can set the boundary to {0, R} because you know that if C is the shorter of the two axes, then 0 < C < R. Solve for C. It takes a while, but you will see the solution:

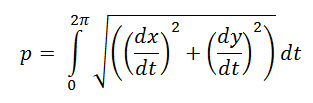
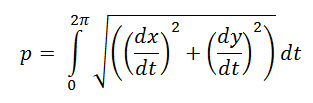
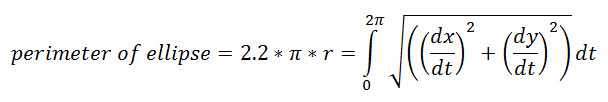
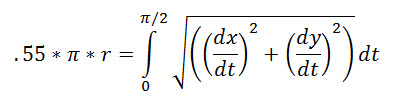
			Y1-.55πR=0
·			C=6.9448351745...
			T=0
			R=10
			bound={0,10}
·			left-rt=0

Now from the home screen, enter:

C				ENTER				6.944835175
R2/C→D				ENTER				14.39918983

Therefore, the half axes of the ellipse have lengths 6.9 cm and 14.4 cm.

Drawing a circle and an ellipse from their parametric description.

Change MODE to Par (parametric) and set it on Radian. Press 6:ZStandard and later 5:ZSquare in ZOOM. Check in 2nd FORMAT that the settings are as follows: RectGC, CoordON, GridOff, AxesON, LabelOff, and ExprOff.
In the Y= editor, enter

\X1T=Rcos(T)				These two equations describe a circle
\Y1T=Rsin(T)				with radius R.
\X2T=Dcos(T)				We switch the position of C and D because it is
\Y2T=Csin(T)				better to have the longer axis of the ellipse along the x-axis.

Now, GRAPH

Use TRACE with the right and left arrows to move around, and use the up and down arrows to jump between the circle and the ellipse. In order to stop tracing, press CLEAR once.
Look at WINDOW, Tmin=0 and Tmax=6.28... If you change these values, for example to -π/2 and π/2, and then GRAPH, you will draw only a part of the circle and a part of the ellipse.

Finally, draw a circle with a compass, and draw the required ellipse with two thumb tacks and a piece of thread. (Or you can get points on its perimeter using lists, as we have done before.)

**********************************************************
Note to those who want to do the problem differently, taking derivatives of trig functions by hand:
The equations, x = c*cos(t), and y = d*sin(t), where t changes from 0 to 2π, describe an ellipse with axes having lengths 2c and 2d. The derivatives are dx/dt = -c*sin(t) and dy/dt = d*cos(t).
In order to find c and d, for the required ellipse we need to solve for c the following equation:

Just as above, we can speed up the process of computation if we compare 1/4 of the perimeters, because it is faster to compute an integral for a smaller range of t. Also, we don't need a negative sign in front of c. So we have

Program for the TI-84.
(In this example, in order to be concrete, we use r = 10 cm.)
Enter
\Y1=fnInt(√((Csin(T))² + (R²/Ccos(T))²),T,0,π/2)
Use Solver to enter the equation, eqn:0=Y1-.55πR, the value of R, and to initialize T and C. You can set the boundary to {0, R} because you know that if C is the shorter of two axes, then 0 < C < R. Solve for C. You will see the solution:

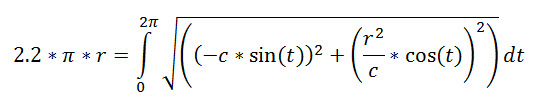
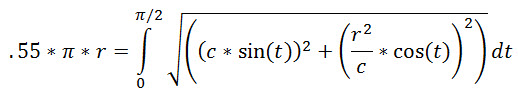
			Y1-.55πR=0
·			C=6.9448351745...
			T=0
			R=10
			bound={0,10}
·			left-rt=0

This value for C matches the value above, 6.9448351745...