Area Under a Parabola

Consider a parabolic arch (similar to the St. Louis arch, which is not a parabola, but a catenary) with the width of its base B and height H. We want to find a formula for the area under the arch.

Variables

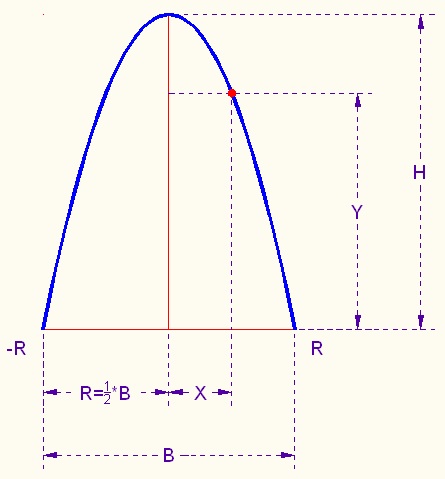
			H				height of the arch
			B				its base
			R = 1/2*B				one half of the base
			X				variable changing from -R to R
			Y				height of the arch above point X on its base

We know that a parabola is a quadratic of the form y = aX² +bX + c. If we can find 3 points on a given parabola that satisfy a quadratic, we know we have the right quadratic for the parabola. We have three points on the parabola above: (x,y) = (-R,0); (0,H); and (R,0). Can we find values a, b, and c above such that our three points satisfy the equation?
We claim that it is this formula, which is a quadratic in X:

Y = H - (H/R2)*X2

(You can check it by plugging in -R, 0, and R for X, and getting 0, H, and 0 for Y.)
Why is this so?

Why does the parabola above have the equation
Y = H - (H/R²)*X²?

We know that the equation of a parabola is y = aX² + bX + c. In the equation above,
a = -(H/R²), b = 0, and c = H.
Our parabola goes through 3 points: (-R, 0), (0, H), and (R, 0).
This means that when we substitute these values for x and y in the equation
y = ax² + bx + c,
the equality holds.
So let's do it, and solve for a, b, and c. Our first point is x = -R, y = 0. We have
y = ax² + bx + c, so our first equation is
0 = R²*a + Rb + c
Next, x = 0, y = H. So our second equation is
H = 0*a + 0*b + c
Finally, x = R, y = 0, so our third equation is
0 = R²*a - Rb + c

So we have three equations in three unknowns, a, b, and c:
0 = R²*a + Rb + c
H = 0*a + 0*b + c
0 = R²*a - Rb + c

Immediately we see that c = H .
So we substitute c = H in the other two equations, and we have :

0 = R2*a + Rb + H				(1)
0 = R2*a - Rb + H				(2)

Adding the two equations, we have
0 = 2R²*a + 2H
Solving this equation for a, we have
a = -H/R².

Now subtracting equation (2) from equation (1), we have
0 = 2Rb
Solving for b, we have
b = 0

Putting this all together, we have
a = -H/R², b = 0, c = H.
So the equation for our parabola is
y = -H/R²x² + H.
It goes through the three points (-R, 0), (0, H), and (R, 0).

Now back to our problem: the area A under the parabola:

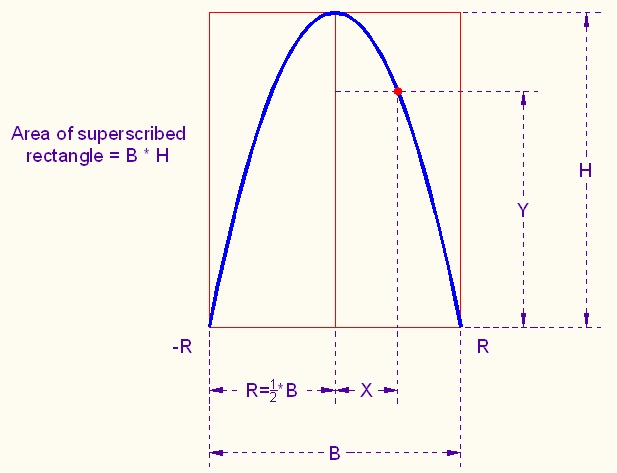
			area	A = the integral of Y dX, for X changing from -R to R.
				A = -R∫RY dX

See this by using vertical slices of the area below the arch.

The area of a rectangle (superscribed on the arch) with base B and height H is

B*H = 2*R*H

Method.

We compute values of A and 2*R*H for several values of R and H , and see whether we can guess a general formula .

Program.
Define,

\Y1=H-(H/R2)X2				height Y
\Y2=fnInt(Y1,X,-R,R)				area under the parabola

Set MODE to Float 4.
From the home screen, run for several specific values r and h,
r→R:h→H:{Y2,2RH}

Example of a table.

R				H				Y2				B*H
1				2				2.6667				4.0000
2				2				5.3333				8.0000
1				3				4.0000				6.0000
2				3				8.0000				12.0000

.....................
It is not hard to guess that the area under a parabolic arch with base B and height H is 2/3*B*H (two thirds of the area of the circumscribed rectangle).

Remarks.
After students learn algebraic methods of computing integrals based on the Fundamental Theorem of Calculus, they will be able to derive the formula Y=(H-R²)*X² and prove that it is correct.
Numerical computation of integrals often allows us to find useful formulas. But proving their correctness requires other techniques.

---

Webpage Maintained by Owen Ramsey
Calculus Index