Rectangle in a Quarter Circle

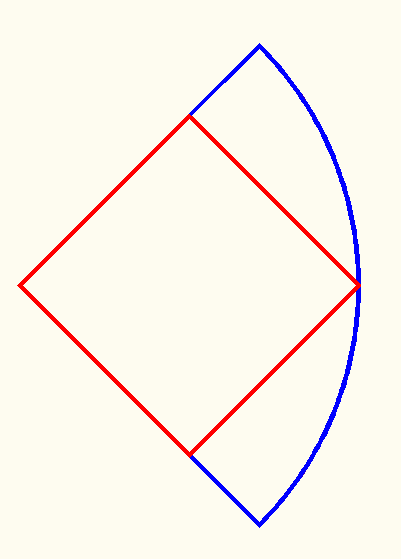
Rectangle in a quarter circle (and square in a quarter circle)

Using two-color poster board, make a large quarter circle. Now design the biggest rectangle possible that just fits in the circular quadrant, oriented as shown in the figure above on the left. Cut apart the four pieces and use them for a puzzle.

Make another quarter circle of the same size, and put in it the largest square possible, as in the figure above on the right. Again cut out the pieces to make a puzzle.

Do the rectangle and the square have the same area? If not, which is bigger? What is the ratio of the areas of the rectangle and square?

Solution for the rectangle:

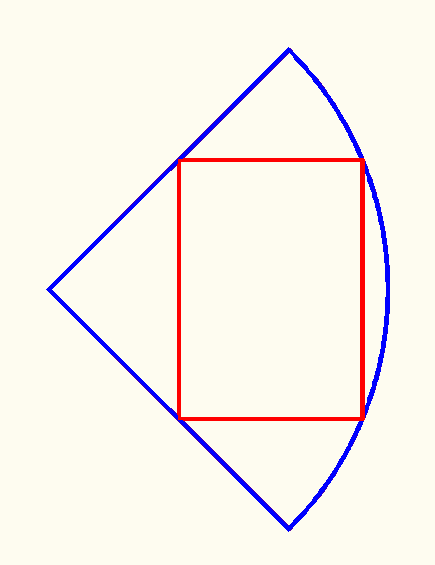
Notice that it is required that two vertices of the rectangle lie on the circumference of the circle. So it is easy to see (by rotating the rectangle) that one side, which is a chord of the circle, is perpendicular to the bisector of the right angle of the quarter circle. (We choose the angle bisector as the x-axis, and we choose the origin at the center of the circle.) So it is enough to view one half of the original quadrant. We first concentrate on the upper half of the rectangle.

The top left upper corner of the rectangle actually lies on the radius r of the circle. We name the coordinates of the corner (y,y). (Do you see it? It is because the angle measures 45°.)

We introduce as a variable angle t, which is the angle between the x-axis and the segment ((0,0), (x,y)) (see figure above). Then
cos(t) = x/r, so
x = r*cos(t)
sin(t) = y/r, so
y = r*sin(t)
Name the horizontal side of the rectangle z. Then
z = x - y = r*cos(t) - r*sin(t).

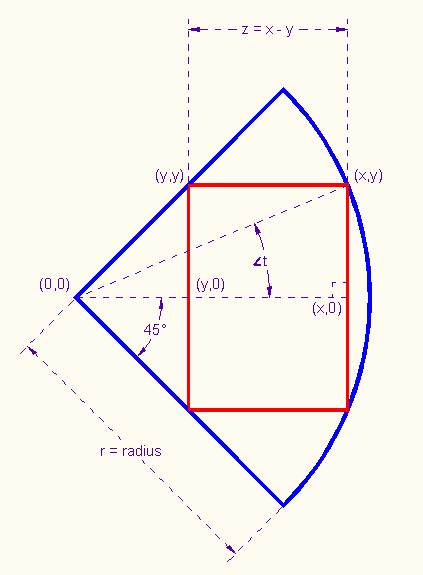
What is the ratio of the area A of the whole rectangle to the area of the quarter circle?
The whole rectangle has area 2*y*z. The quarter circle has area 1/4 * π * r². So

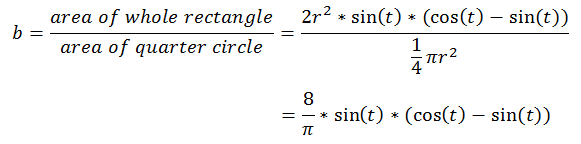
We want to maximize this ratio. So we need to find for which value of t its derivative with respect to t equals 0.
Under MODE, choose DEGREE.
We can rename variable t as X. Enter
Y₁=(8/π)*sin(X)*(cos(X)-sin(X))
Then use SOLVER (under MATH).
Under EQUATION SOLVER,
eqn:0=nDeriv(Y₁,X,X)
Press ENTER, and you will see
nDeriv(Y₁,X,X)=0
X= (something) (enter a guess, between 0 and 45 degrees).
Set bound to
bound = {0,1E99}
Put the cursor in the X= row and press ALPHA SOLVE. You will see X=22.500000004.
So angle t above = 22.5°.
To find the ratio of the area of the whole rectangle to the area of the quarter circle, on the home screen, enter Y₁ ENTER.
You will see .5273930876.
So the rectangle covers about 53% of the quarter circle.

Let's compute the width z and height y of the rectangle in terms of r.
z = r*(cos(t)-sin(t)), so
z = (cos(22.5°) - sin(22.5°))*r = .5411961001*r, so
z ≈ .54*r
y = r*sin(t) ≈ .38*r

With this information, can you construct the rectangle in the quadrant?

Can you design a square in an identical quadrant?
What is the ratio of the square's area to the area of the quadrant?

What is the ratio of the area of the rectangle to the area of the square?