Rain Gutter

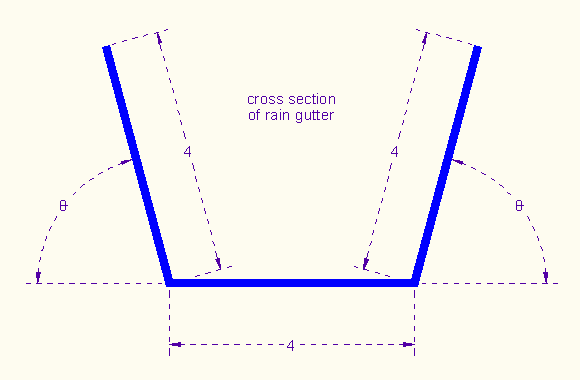
A long sheet of tin 12 inches in width is to be bent to form a rain gutter as shown below. (You have a piece of posterboard of this length!) Determine angle theta so that the gutter will carry the most water, that is, so its cross-sectional area is at a maximum.

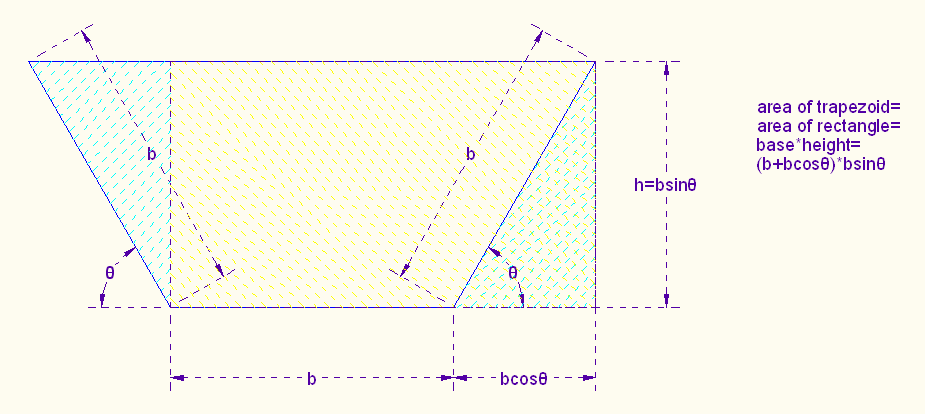
Let's consider a more general case, where the width of the tin is 3b. We transform the trapezoidal cross section above into a rectangle by cutting off the left-most triangle and putting it on the right:

We see that the area of the rectangle is base*height. With a little trigonometry, we see that base*height is (b+b*cosθ)*b*sinθ=b²(1+cosθ)*sinθ=b²(sinθ+cosθ*sinθ)=f(θ).

Task 1. Let's try some values of θ (which we'll now call X) and see what happens. Set MODE to degree. X can range from 0° to 180°. But can you see that if X > 90°, the area gets smaller?

Try this:

From the home screen, enter

"B²(sin(LX)+cos(LX)*sin(LX))"→A

{5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95}→X

"ΔList(LA)/ΔList(LX)"→R

R is a list of rates of change, namely, the difference of two adjacent areas divided by the difference of two adjacent angles.
Now, in STAT Edit, enter:

Name=X
Name=A
Name=R

The three lists will automatically fill. What do you see? How does the area A vary? How is R computed?
Just as with the unit on the open box, you can change the values of X and again go to STAT Edit.

Task 2.
We want the area, f(θ), to be as big as possible. So we take the derivative and set it equal to zero. (First we may take out b², a constant. Or we can leave it in. If we leave it in, we need to assign a value to b on the home screen. We are using a 12-inch wide piece of poster board, so our b is 12/3 = 4 inches. So we may store the value 4 in B: 4→B.)
d/dt(sinθ + cosθ*sinθ) = 0
Press MODE and set the calculator to Degree.
Here is one way to proceed:

In the Y= menu, set

\Y₁=B²(sin(X)+cos(X)sin(X))

Now use Solver:

EQUATION SOLVER
eqn:0=nDeriv(Y₁,X,X) ENTER
B=4
X= (something; here you enter a guess)
bound={-1E99,1E99}

Since X cannot be negative, you may set the bound as follows:

bound={0,1E99}

Make a guess (for example, 45 degrees) for X, and leave the cursor on the X= row.
Press ALPHA SOLVE, and you will see

X=59.999999971637

So the trapezoid has a maximum area when the angle is 60°. But what is the area of the trapezoid when the angle is 60°? On the home screen, enter

Y₁

You will see

20.78460969

Of course, the units are square inches.

For those who know some trigonometric identities, here is another way:

The derivative of sinθ = cosθ.
We use a trigonometric identity: cosθ*sinθ=½sin(2θ).
d/dt(½sin(2θ))=cos(2θ).
So d/dt(sinθ+cosθsinθ) = cosθ + cos(2θ) = 0

We know that cosθ + cos(180 - θ) = 0.
Therefore cos2θ = cos(180 - θ)
So now let's ask when 180-θ = 2θ.
3θ = 180°, so θ = 60°.

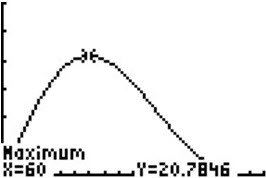
Task 3. you may also investigate when the area of the trapezoid is greatest by setting the window as follows:

Xmin=0
Xmax=180
Xscl=10
Ymin=0
Ymax=30
Yscl=5
Xres=1

Then graph Y₁.

Use CALC to locate the maximum.

So again we see the maximum area is when the angle is sixty degrees.
Here is the rain gutter cross section, drawn to scale:

Can you make your posterboard into a "gutter" with angles to maximize the water flow?