Quadrilaterals

The hands-on part of this unit may be done by either stringing four pieces of straw on a string to make quadrilaterals or by drawing quadrilaterals using ruler and compass. Students seem to prefer doing it with straws, so in I we use straws with lengths 6, 7, 9, and 11 cm. In II we actually draw the different quadrilaterals with the same four side lengths, 6, 7, 9, and 11, and we ask the same questions. The mathematics is the same.

I. Using straws.
Supplies: drinking straws, string, scissors.
We start by making quadrilaterals with four pieces of straw, whose lengths are 6, 7, 9, and 11 cm, and string (as in the picture).
Our first question is, how many different ways are there to string the four straws? (See "Remark" in Task 2 below.)
The second question is, for each way to string the pieces, how do you arrange the angles so that the quadrilateral's area is as large as possible? (See Task 3 below for a method to determine this.)
The third question is, is the maximal area with one way of stringing the same as or different from another way of stringing? See Tasks 3 and 4 below.
Questions asked in the remaining tasks, 5, 6, and 7, are also applicable to part I.

II. Using ruler and compass.
Task 1.
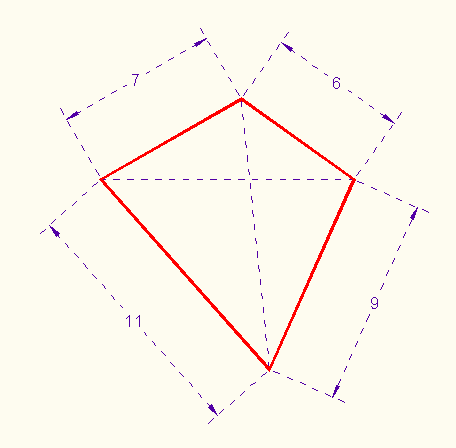
Draw a convex quadrilateral with sides 6 cm, 7 cm, 9 cm, and 11 cm. Make the necessary measurements, and compute its area.
Here is one:

Remarks.
We will use variables that can be directly entered into the TI-84. There are many quadrilaterals with these sides. Choose one that you like.

Method.
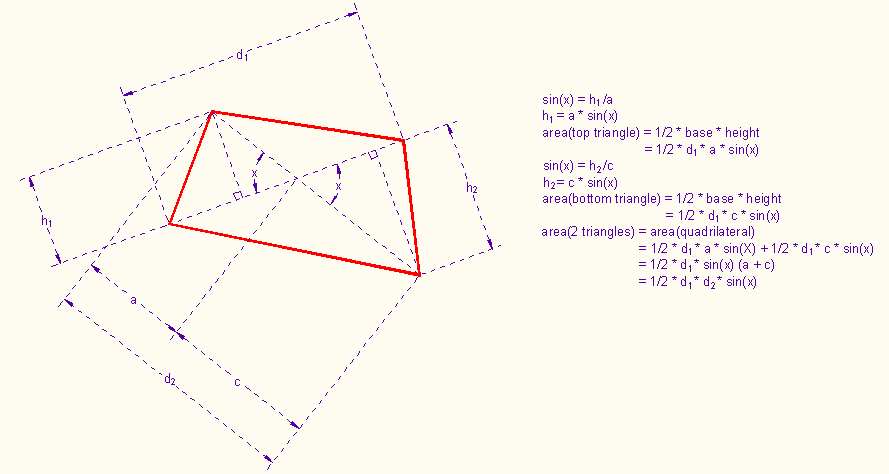
The simplest way to compute the area S of a convex quadrilateral is to measure its diagonals F and G, and the angle X between them, and compute S = .5*F*G*sin(X).

Can you prove the correctness of this formula? Here is a derivation.

Task 2.
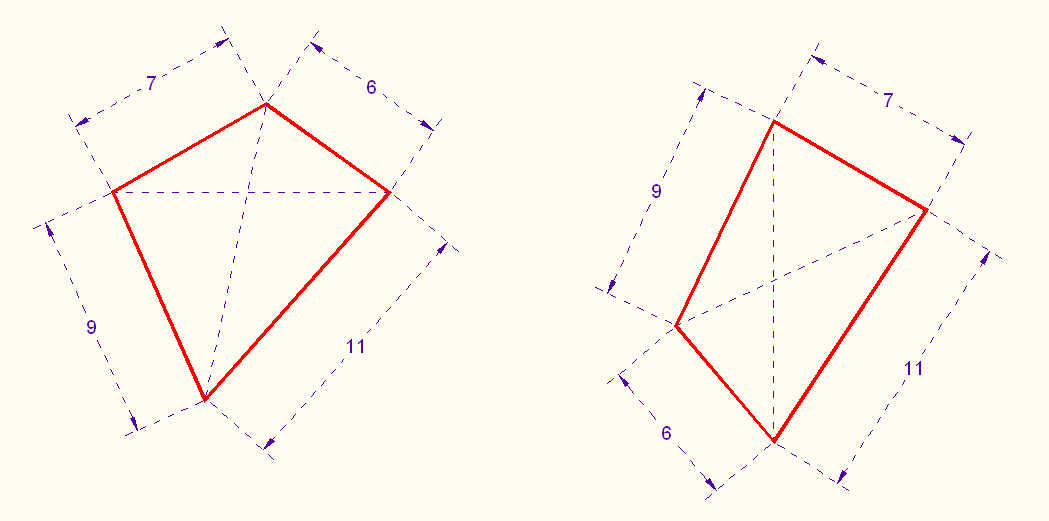
Draw two other (non-congruent) quadrilaterals with the same sides and the same area.

Method.
It is easy. Designate one of the diagonals of the original quadrilateral as the base of its two triangles, and just flip two adjacent sides of the quadrilateral. (See picture.) That gives you one new quadrilateral. Next do the same for the other diagonal.

Remark.
There are three different quadrilaterals with the same area. One has sides in the following order: 6, 7, 9, and 11; the second has them in the order 6, 7,11, and 9; and the third, 6, 9, 7 and 11.

Task 3.
Design, neatly draw, and also cut out from construction paper three different quadrilaterals (with edges specified as above) that have the biggest possible area.

Method.
1. Whenever the values of a function f(x) change gradually, the rate of change is 0 for those x's for which f(x) is maximal or minimal. (The rate of change passes through 0, when it switches from positive to negative, or from negative to positive.) Thus the most common way to look for maxima and minima is to solve an equation, nDeriv(f(X),X,X) = 0. (Remember that the numerical derivative computes the rate of change of the function f(X).)

2. Let's choose the length of one diagonal of the quadrilateral with sides A, B, C, and D as the variable X. Then the quadrilateral can be viewed as two triangles, one with sides A, B, and X, and the other with sides C, D, and X, By Heron's formula, its area is
S = √((X+A+B)(-X+A+B)(X-A+B)(X+A-B))/4 + √ ((X+A+B)(-X+A+B)(X-A+B)(X+A-B))/4

3. The following program allows you to find the values of the diagonals of all three quadrilaterals with maximal areas.

\Y₁=√ ((X+A+B)(-X+A+B)(X-A+B)(X+A-B))/4 +√ ((X+C+D)(-X+C+D)(X-C+D)(X+C-D))/4
(Can you derive this formula from the more common formulation of Heron's formula for the area of a triangle, which is
area of triangle = √(s*(s-a)*(s-b)*(s-c)), for a triangle with sides a, b, and c, and where the semi-perimeter s is defined as s = (a + b + c)/2? (In Y₁ above, the area of a quadrilateral is written as the sum of two triangles.))

Let's work first with the quadrilateral with side lengths (listed consecutively) 7, 6, 11, 9.
In Solver, enter eqn:0=nDeriv(Y₁,X,X), and edit the values of variables, and you will get:
nDeriv(Y₁,X,X)=0
A=7
B=6
X= something (put in a guess)
C=9
D=11
bound={-1e99,1...

Put the cursor on the X= line, and press [ALPHA][SOLVE].
You will see X=10.94765098112

Here, we are looking at the triangles A=7, B=6, X, and C=11, D=9, X. In order to get the other diagonal in this quadrilateral, switch the values of A, B, C, and D in the solver. You may use A=7, B=9, X; and C=11, D=6, X. The solver gives
X=11.96603716757.
Now you have the lengths of the diagonals of one quadrilateral with maximal area: 10.95 and 11.96 cm.

There are two more quadrilaterals with maximal area. (Do you see why?) Their sides are (listed consecutively) 7, 11, 6, 9; and 7, 11, 9, and 6.
Using solver again, you will find, for the 7, 11, 6, 9 quadrilateral, the diagonals have lengths 11.78 cm and 11.96 cm.
For the 7, 11, 9, 6 quadrilateral, the diagonals have lengths 11.78 and 10.95 cm.
So there are only three different lengths of diagonals. But they combine in pairs to make three different quadrilaterals.

Store the values of the diagonals in E, F, and G for future use.

Graph Y₁. Can you see where it has the biggest value? Why do the values of Y₁ have such a limited range? (Use TRACE, and 2nd CALC)
Using VARS, put Y₁ on the home screen and press [ENTER]. You will see 64.15, the area of the quadrilateral in square centimeters.
Remark.
Most of the time you can just use graphing to find maxima and minima of a function. But students should understand that the underlying computation uses the numerical derivative, and that the graphing facility only displays the results.
Drawing a quadrilateral when the lengths of a diagonal and four sides are given.
The diagonal splits the quadrilateral into two triangles. Draw the diagonal and use it as the base of the two triangles.

Task 4.
Measure and compute the areas of your quadrilaterals to find how good the match is between the theoretically predicted area and the measured area. You may use the formula above: The simplest way to compute the area S of a convex quadrilateral is to measure its diagonals F and G, and the angle X between them, and compute, S = .5*F*G*sin(X).

Task 5.
Measure all angles of your quadrilaterals. Add each pair of opposite angles. What do you observe? (The sums are close to 180 degrees. This is a proven theorem. In a quadrilateral with the biggest possible area for its sides, the sum of the opposite angles is 180 degrees.)

Task 6.
Try to circumscribe a circle around your quadrilateral. Can it be done?
(Yes, there is a theorem that says that a circle can be circumscribed around a quadrilateral if and only if its opposite angles add up to 180 degrees.)
To circumscribe a circle around your quadrilateral, construct the perpendicular bisectors of two sides, and where they intersect is the center of the circle.

Remarks.
The task of drawing a quadrilateral with given sides inscribed in a circle can be solved by drawing a quadrilateral with biggest area (by the method shown above) and circumscribing a circle around it. Why does it work? (By the theorem quoted in task 6.)
"Doing mathematics" is 99% knowledge and 1% ingenuity.

Task 7.
Compute:
√ ((-A+B+C+D)(A-B+C+D)(A+B-C+D)(A+B+C-D))/4
(You get the area S of your quadrilaterals. It is Heron's formula for the area of a quadrilateral inscribed in a circle.)