Privateer problem

---

Here is a problem from Differential and Integral Calculus with applications by

William S. Hall, 1897. It is not "hands on", but the trick below that is used to solve it is pretty cool.

Here is really easy way to look at the privateer problem. We have the following two equations:

Let x equal the distance from A on the line AB. Then

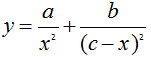
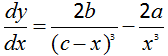
(If you do not know how to take the derivative by hand, you can find it at wolfram alpha, http://www.wolframalpha.com/input/?i=derivative.)

We set the derivative equal to zero to find where the function is at a minimum:

We can divide the equation by 2:

Now we have a trick; we define

and

So

So

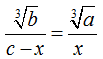
We cross-multiply:

Then

So we get the answer given in the 1897 book!

Here is another approach, using the TI-83/84 calculator:

Let x be the distance from A.

Then we have

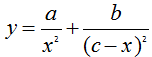
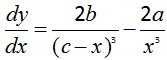
We need to set this equal to zero and solve for x.

The problem is the three varaiables, a, b, and c. How to solve it?

Thanks to my friend, I have an approach. (And I do not need to compute dy/dx.)

Assign randomly 3 values to a, b, and c. Store the values for a, b, and c in the variables A, B, and C in the TI-83/84. For example,

5→A:7→B:3→C

1. Put this equation in Y1:

Y1=A/X²+B/(C-X)²

Now go to solver.

EQUATION SOLVER

eqn:0=nDeriv(Y1,X,X)

ENTER

You will see

nDeriv(Y1,X,X)=0

A=5

X=(something)

B=7

C=3

bound={-1E99,1E99}

(You may change this to

bound={0,1E99}.)

Put in some guess for X, say 1, and press ALPHA SOLVE. You will see

X=1.4159700587

2. Using the TI-83/84 again, put the values for a, b, and c in the formula in the book, and get a value for x. (Put this equation into the TI 83/84 calculator:

Y2=CA^(1/3)/(A^(1/3)+B^(1/3))

Now from the home screen enter Y2.

You will see 1.41597009

Store new random values in A, B, and C, and repeat steps 1 and 2. Do this several times. If your values in the two steps are equal, you can begin to believe that the formula in the book is correct.

---

Webpage Maintained by Owen Ramsey
Calculus Index