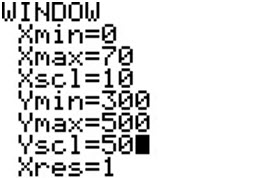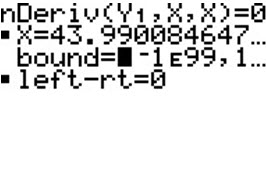A Piece of Wire

A piece of wire

You have a piece of plastic-covered clothesline wire one meter long. Your task is to cut the wire into two pieces, one of which you form into a square and the other into a circle, so that the sum of the areas of the two figures is (a) as big as possible; (b) as small as possible.

Sketch of a solution.

Let the side of the square be s and let the radius of the circle be r. Then the perimeter of the square is 4s, and the circumference of the circle is 2*π*r.
The sum of the two perimeters is 100 cm:
4s + 2*π*r = 100.
Solving for s,
s = 25 - π*r/2

The total area of the two figures is s² + π*r². Substituting in 25 - π*r/2 for s,
total area A = (25 - π*r/2)² + π*r².

Do you know what to do next?

When the area is at a minimum, r = 7.0012394191 cm. What is s?
When the area is at a maximum, r = 15.91549431 cm. What is s? Why?
Be sure to cut the wire and form your circle and square! You will notice something interesting when you get the figures made.

If the wire were 60 cm in length, how would you cut it?
******************************************************************

One way to solve the problem:

We use X for the radius r of the circle. In Y= we enter:
\Y₁=(25-πX/2)²+πX²
We want to find where the rate of change of this function is zero.
In Solver,
eqn:0=nDeriv(Y₁,X,X)
In X= enter some reasonable guess, and press ALPHA SOLVE.
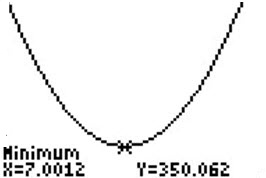
You will see:
X=7.0012394196
From the home screen, enter Y₁ and you will see
350.06197009
So the total area, when it is at a minimum, is 350 sq. cm.

Another way:

Again we use X for the radius r of the circle. In Y= we enter:
\Y₁=(25-πX/2)²+πX²
and we set WINDOW
Xmin=0
Xmax=15
Xscl=5
Ymin=300
Ymax=600
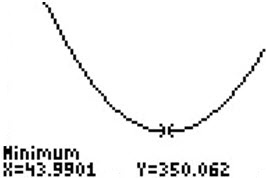
We then graph, and use CALC minimum.

A third way, with lists.

From the home screen,

"(25-πLX/2)²+πLX²"→A

"ΔList(LA)/ΔList(LX)"→R

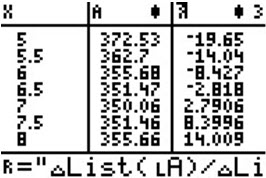
Choose some values for X (radius of the circle in centimeters. For example,

{5,5.5,6,6.5,7,7.5,8,8.5,9,9.5,10}→X

Now go to STAT Edit and enter X, A, and R.
Look at where the value for A has a rate of change of zero:

It is between 6.5 and 7.5.
Try again with new values of X between these two values.

A fourth way (for those who have studied calculus before)

We have
y=(25-πx/2)²+πx²
Multiply this out and take the derivative by hand:
y=25²-50πx/2+π²x²/4+πx²
=25²-25πx+(π²/4+π)x²
This is a polynomial in x, so
y'=-25π+2(π²/4+π)x
Set this equal to zero, and
25π = 2(π²/4+π)x
Dividing by π, we have
25 = (π/2+2)x
x = 25/(π/2+2)=7.001239419 cm

A fifth way.

Let X be the length of the 100 cm that makes the circle, and 100-X be the length that makes the square. Then
circumference c of circle=2πr=x,
so r=x/(2π).
perimeter p of square = 4s = 100-x,
so s = (100-x)/4.
area of circle = A_circle = πr² = π(x/(2π))² = x²/(4π)
area of square = A_square = ((100-x)/4)²
We want A_circle + A_square = x²/(4π)+((100-x)/4)² to be as small as possible.

We enter
\Y₁=X²/(4π)+((100-X)/4)²
Then set window:

and graph:

Use CALC to find the minimum:

Or use SOLVER and nDeriv:

Extra credit. Cut a 1-meter long wire into two pieces to make a circle and an equilateral triangle such that the sum of the areas of the two figures is as small as possible. Show how you did it.
More extra credit. Can you find a general rule for making any regular polygon and circle from a given length of wire, such that the sum of the areas of the two figures is as small as possible?