More on the Wire Problem
After finding the
sizes of a circle and square which have the smallest combined area and the sum
of perimeters having length L, we can ask some "follow up" questions.
(In the task we were given, a piece of wire of length L was given and a square
and a circle had to be made from this wire.)
One question is about a generalization of this task. What if we were required
to make a circle and equilateral triangle, or a circle and another regular
polygon? What if we were required to make two regular polygons, for example, an
equilateral triangle and a regular hexagon?
The same "general" technique solves all these problems, but finding
relationships between the perimeter Pn and area An of a
regular n-gon (an n-sided polygon) requires trigonometry.
Basic facts.
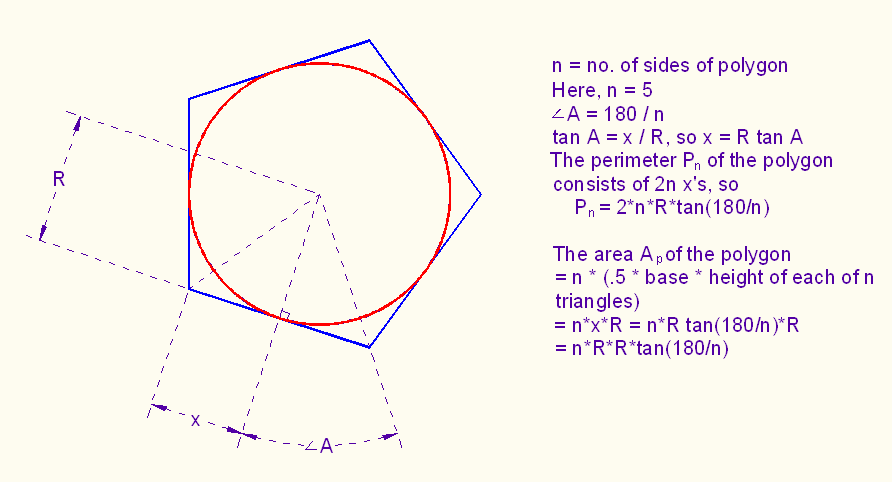
Let R be the radius of a circle inscribed in a regular n-gon. Then
Pn = 2*n*R*tan(180/n) (1)
where the angle is measured in degrees.
[see the drawing below for an explanation]
An = n*R*R*tan(180/n) (2)
(n times height times 1/2 base of a triangle, which is 1/n of the polygon)
[again, see drawing below]
So R = Pn/(2*n*tan(180/n)),
and substituting it to the second equation we get a relationship between An
and Pn,
An = Pn2/(4*n*tan(180/n))
But there is one "surprising" fact about the square and circle
problem. The diameter of the circle and the side of a square are the same! Such
"coincidences" are rarely accidental. Does it also generalize?
Remark
There are situations when forming a hypothesis is easy, but proving it is very
difficult. But here we face the opposite. After we guess the right hypothesis,
its proof is not difficult. But the right guess is not obvious.
In our solution the square can be circumscribed on the circle (the circle is
inscribed in the square). So this is going to be our hypothesis.
Hypothesis
When we have a regular n-gon and a circle with the smallest total area, when
the sum of their perimeters is given, then the n-gon can be circumscribed on
the circle.
Proof.
Variables:
|
||
r
|
radius of circle
|
|
P = 2*π*r
|
its perimeter
|
|
A = P2/(4*π)
|
its area
|
|
n > 2
|
number of sides of the regular n-gon
|
|
R
|
radius of the circle inscribed in n-gon
|
|
Pn
|
n-gon's perimeter
|
|
An
|
its area
|
|
L = P + Pn
|
given sum of perimeters (length of wire)
|
dAn/dPn = Pn/(2*n*tan(180/n))
= R
|
see [1] below
|
{5}
|
dA/dP = P/(2*π) = r
|
see [2]
|
{5}
|
Pn = L - P, therefore dPn/dP = -1
|
see [3]
|
{4}
|
Also,
|
||
dAn/dP = dAn/dPn * dPn/dP
= -dAn/dPn
|
(multiplication of fractions)
|
|
see [4]
|
{5}
|
|
The minimum area is achieved when,
|
||
d(A + An)/dP = 0
|
||
But,
|
||
d(A + An)/dP = dA/dP + dAn/dP =
dA/dP - dAn/dPn = r - R
|
see [5]
|
|
Thus, r = R, which means that the circle inscribed in the
n-gon has radius r.
|
||
That proves our hypothesis.
|
Computation.
We want to compute what percentage of L is taken up by the perimeter of a
circle for a given n = 3, 4, ... .
We have,
L = P + Pn = 2*π*r + 2*n*R*tan(180/n) = (2*π+
2*n*tan(180/n))*r
So,
r = P/(2*π + 2*n*tan(180/n)) and 2*π*r/P = (1 + n*tan(180/n)/ π)-1
Remark
n*tan(180/n)/π is less mysterious if you know how Archimedes approximated
π by constructing polygons circumscribed on a circle. When n increases,
n*tan(180/n)/π converges to 1.
Program.
Set MODE to Degree and Fix 3.
Define:
\Y1=(1+Xtan(180/X)/ π)^-1
seq(Y1,X,3,10)→L1 ENTER
L1 ENTER
You will get:
{.377 .440 .464 .476 .482 .487 .490 .492}
Convergence is very slow.
Y1(20)
|
ENTER
|
|
.498
|
||
Y1(30)
|
ENTER
|
|
.499
|
||
Y1(40)
|
ENTER
|
|
.499
|
||
Y1(50)
|
ENTER
|
|
.500
|
******************************************************************************
[0] We want to show that A = P2/(4π).
We know A = πr2. But this equals 4π2r2/(4π)=P2/(4π).
[1] We had above, An = Pn2/(4*n*tan(180/n)),
and therefore
dAn/dPn = (2*Pn)/(4*n*tan(180/n)) = Pn/(2*n*tan(180/n))
We also had, R = Pn/(2n tan(180/n)).
[2] We had A = P2/(4*π), so dA/dP = 2*P/(4*π) =
P/(2*π).
[3] Pn = L - P, so dPn/dP = dL/dP - dP/dP. But L is
constant so dL/dP = 0,
and dP/dP = 1. Therefore dPn/dP = 0 - 1 = -1
[4] Why is (dZ/dY)*(dY/dX) = dZ/dX?
Consider three lists LX,
LY, and LZ.
The rate of change of Z relative to Y is ΔList(LZ)/ ΔList(LY).
The rate of change of Y relative to X is ΔList(LY)/ ΔList(LX).
The rate of change of Z relative to X is ΔList(LZ)/ ΔList(LX).
Check that,
(ΔList(LZ)/ ΔList(LY))*( ΔList(LY)/ ΔList(LX)) = ΔList(LZ)/ ΔList(LX).
If your car uses p gallons of gas per mile (I hope that p << 1) and you
drive with a speed of q miles per hour, then you car uses p*q gallons of gas
per hour.
In the case at hand, we have dAn/dP = (dAn/dPn)*(dPn/dP).
But we had above
dPn/dP = -1, so dAn/dP = - dAn/dPn.
[5] We had dA/dP = r, we had dAn/DPn = R, and we had dAn/dP
= -dAn/dPn.
So d(A + An) = r - R, as shown above in the text.
General remark.
I expect that the students who do not make models or very precise drawings have
no chance of forming the hypothesis we have proven.
Calculus Index