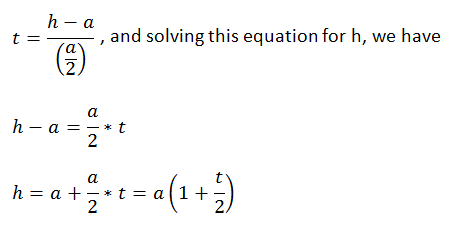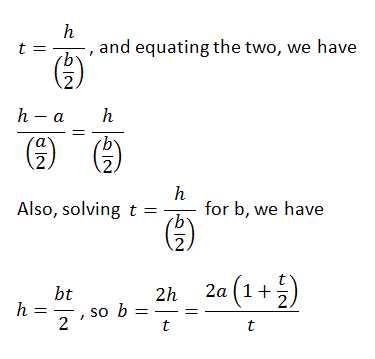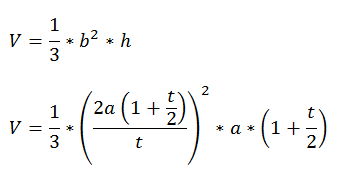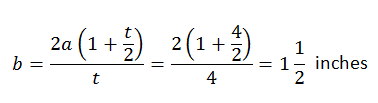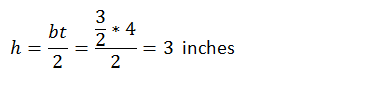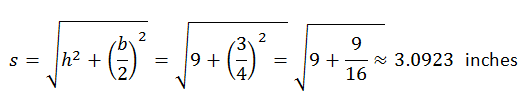Cube in a Pyramid

Task.
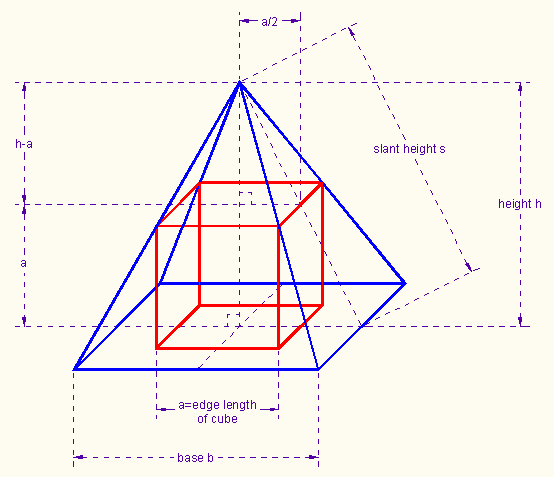
You are given a cube. Design and construct a pyramid with square base that fits over the cube, touching its four top edges. The pyramid should have volume as small as possible.

Solution.

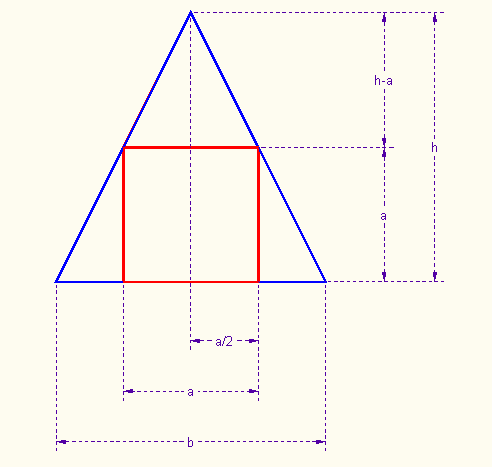
We measure the edge length a of the cube.
We define a new independent variable t as follows:

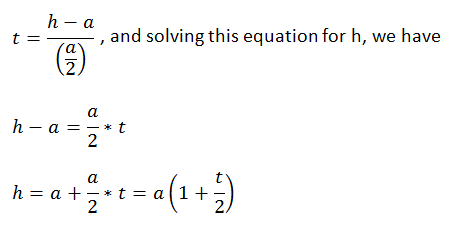
t is the ratio of two legs of a right triangle (see illustration above).
But notice, because of similar triangles, that

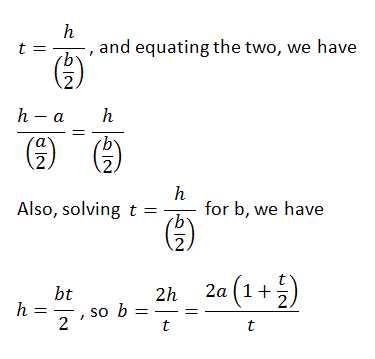
Now we have both b and h in terms of t (which we want to find) and a (which we know).

The volume V of a pyramid is 1/3*(area of base)*height. Our goal is to make V as small as possible for our given a.

We can write the volume in terms of a and t:

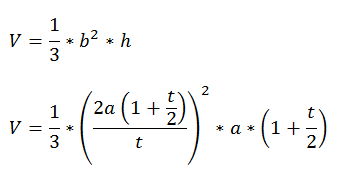
So,

This is the volume that we want to minimize. We will do this in several ways.

Method 1: Using nDeriv
First we measure the edge length a of our cube. We store this value in a. Here we used cubic inch blocks, so
1→A
In the above formula for V, we use X for the independent variable (it is easier to use than T).
Enter
\Y₁=(4/3)*A³*(1+X/
2)³/X²
Go to MATH and then select SOLVER. Press the up-arrow, and you will see
EQUATION SOLVER
eqn:0=
Enter
eqn:0=nDeriv(Y₁,X,X) ENTER
You will see
nDeriv(Y₁,X,X)=0
A=1
X= (something)
bound={-1E99,1E99}
Set the bound to
bound={0,1E99}
X is the ratio of the height of the pyramid to half of its base. So what is a good guess for this ratio? Let's try 2.
X=2
Leave the cursor on the X=2 line, and press ALPHA SOLVE.
You will see
X=4.0000001388215
So h/(b/2) = 4, and thus
h = 2*b
So the height of the pyramid is twice the base.
What is the volume of the pyramid? On the home screen, enter Y₁ ENTER
Y₁=2.25 cubic inches.
So the ratio of the volume of the pyramid to the volume of the cube is 2.25. (This ratio will hold for any cube!) The cube fills .444 of the pyramid, a little less than half.

Method 2. Graphing.
Set WINDOW:
Xmin=0
Xmax=12
Xscl=1
Ymin=0
Ymax=6
Yscl=1
Xres=1
Then graph Y₁.
We want to find where the Y-value of this graph is at a minimum.
2nd CALC
minimum
You need to choose a left bound and a right bound, and guess a minimum. Then press ENTER.
Minimum
X=4.0000004 Y=2.25

Method 3. Using lists to find where the rate of change is 0.
{.25,.5,.75,1,1.25,1.5,1.75,2,2.25,2.5,2.75,3,3.25,3.5,3.75,4,4.25,4.5,4.75,5,5.25,5.5,5.75,6}→X
"4/3*A³*(1+LX/2)
³/LX²"→V
"ΔList(LV)/ΔList(LX)"→R
R is a list of rates of change, namely, the difference of two adjacent volumes divided by the difference of two adjacent ratios of height to one-half of base (our variable X).
Now in STAT Edit, you may first clear out old lists by pressing DEL. Then enter:
Name=X
Name=V
Name=R.
The three lists will fill. Investigate where R is close to zero.
You will see that when X=4, V=2.25.
You can put in new values for X, slightly less than and greater than 4, to investigate this.

Is this cool, or what??

Okay, now we have to figure out how to design our pyramid!

Our pyramid will have a square bottom face, and 4 lateral faces that are congruent isosceles triangles.
1. Compute the edge length b of the base.
We know X (originally our t) is 4, and a is 1 inch.

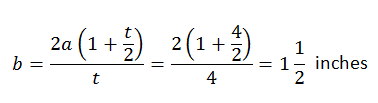
2. Now let's find h.

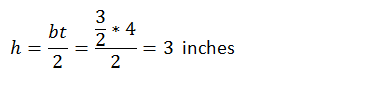
3. In order to design the triangular faces of the pyramid, we need to find s, the slant height of the pyramid. It is also the height of a triangular face. (See the first diagram in this unit, where the slant height s is labeled.)

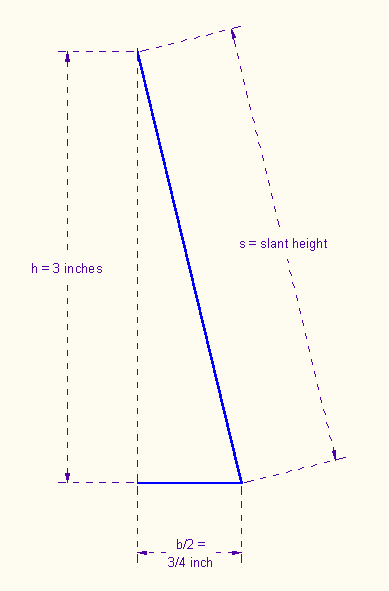
We use the Pythagorean theorem to find s:

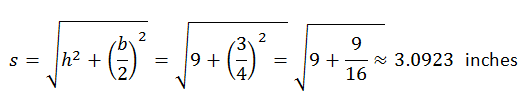
4. Now we need to find the edge length e of the isosceles triangles. See the next illustration. Again we use the Pythagorean theorem.

Finally we can design our net for the pyramid. Do you need help with this? You can do it without finding any angles in the triangles, but I found it easier to find the top angle. (I used tan^-1(.75/3.09) = angle P.)
Here is my net:

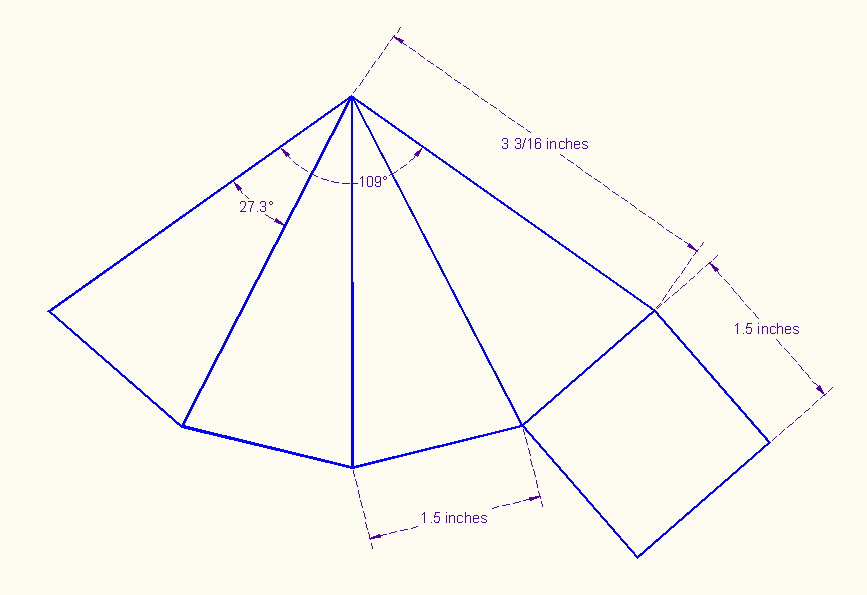
Do you see how to design it?