Cone with maximal volume

 

Task.

Design and make from poster board a cone with a slant height S equal to 10 cm. The cone should have the biggest volume possible.

 

Solution

The volume V of a cone with height h and radius r is given by V=1/*3πr2h.

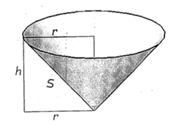
But S2= h2 + r2, so r2 = S2 - h2

So,

 

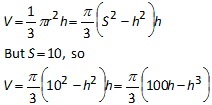
We want to maximize this volume.

Let's use solver and nDeriv, to solve for h. (We now call it X.)

We put in Y1:

\Y1=(π/3)*(100X-X3)

Then in solver,

eqn:0=nDeriv(Y1,X,X)

We have to make a guess for X (the cone's height). It will be less than 10.

Then we press alpha solve

We get X=5.7735026629… This is the height h of the cone.

 

What next?

We need to find the radius of the cone. We use the Pythagorean theorem:

r2 + h2 = S2

r2 = S2 - h2

r = √ ( S2 - h2)

S = 10, so

r ≈ 8.14619… cm

 

 

 

 

How to design the cone?

A cone is made from a sector of a circle, so we need to find how many degrees are in the sector, namely, in the angle we will call A. Our circle will have a radius S of 10 cm, which is the slant height of the cone.

 

 

 

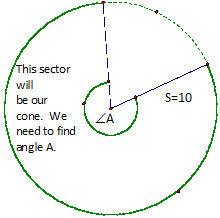
Here is the equation we need to solve:

 

angle A/360°= (2πr)/(2π S)

So

angle A = (r/S)*360°.

Do you see it?

We have r and S, so let's solve the equation for angle A!

Now we can build our cone!

 

What is the volume of the cone?

From the home screen, enter

Y1.

Webpage Maintained by Owen Ramsey
Calculus Index