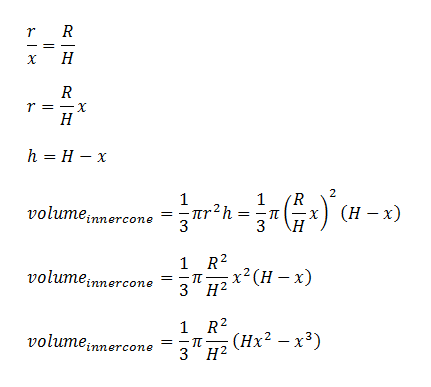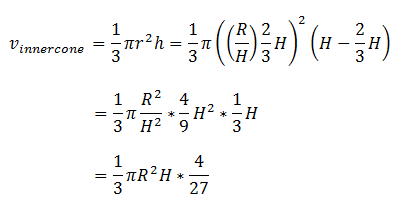Cone in a Cone

You have a birthday hat in the shape of a cone. Make another cone that just fits in the hat and whose vertex is at the center of the base of the hat. The new cone should have the biggest volume possible.
Show how you did it:
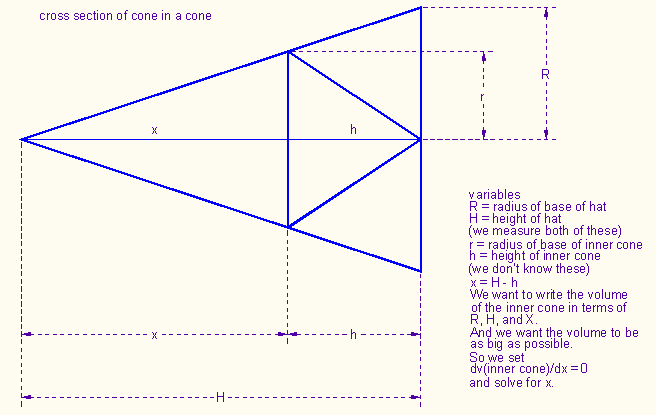
Draw a diagram and label the variables, and give the equations that relate the variables.

What is the ratio of the height of the inside cone to the height of the hat?

What is the ratio of the volume of the inside cone to the volume of the hat?

Outline of a solution.

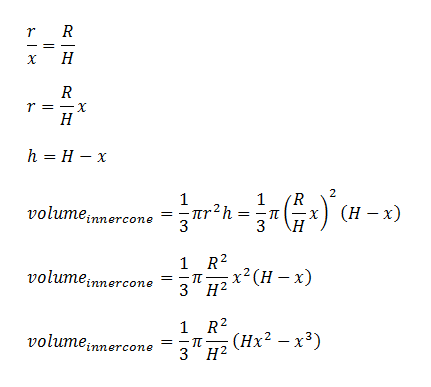
So now we measure the diameter of our hat and its slant height. We divide the diameter by 2 and store that value in R. We use the Pythagorean theorem with R and S to find H. Measuring in centimeters, I got:
5.25→R
15.89→H

You may now use nDeriv and Solver:
(Since (1/3)πR²/H² is a constant, you may leave it out when you look at rate of change.)
Y₁= HX²-X³
In Solver,
Eqn: 0 = nDeriv(Y₁,X,X)
I got
X=10.593333301...
And I note that X/H = 2/3!

Or, if you remember how to take the derivative of a polynomial, we have
y = Hx²-x³, so
dy/dx = 2Hx - 3x², and we set this derivative equal to zero:
2Hx - 3x² = 0
x(2H-3x) = 0
2H = 3x
x = 2/3 H.

Now, can you design your inner cone?

What about the ratio of the volume of the inner cone to the outer cone?

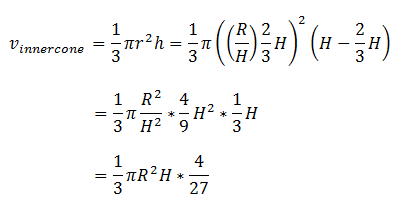
So the small cone has 4/27 the volume of the big cone!

Cheat sheet for constructing a cone in the birthday hat such that the cone has the biggest volume possible

Compute the radius R and height H of your birthday hat. (Find the height by measuring the slant height and radius and using the Pythagorean theorem!) I got R=5.25 cm, H=15.89 cm. Also compute x = 2/3*H.
We note that the height h of the inner cone = 1/3*H (since x = 2/3*H).

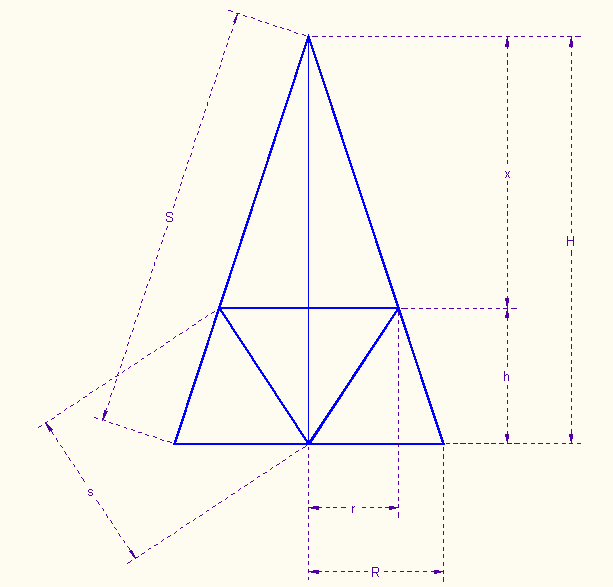
Using similar triangles, r/x = R/H, so
r = R/H*x.
Now we need to find s, the slant height of the inner cone. Again we use the Pythagorean theorem. We know r and h, so s = √(r²+h²)
s is the radius of the sector we need to cut to make the cone. We need to find the angle A of the sector.
The circumference of the sector is 2πr, and the circumference of the whole circle is 2πs.

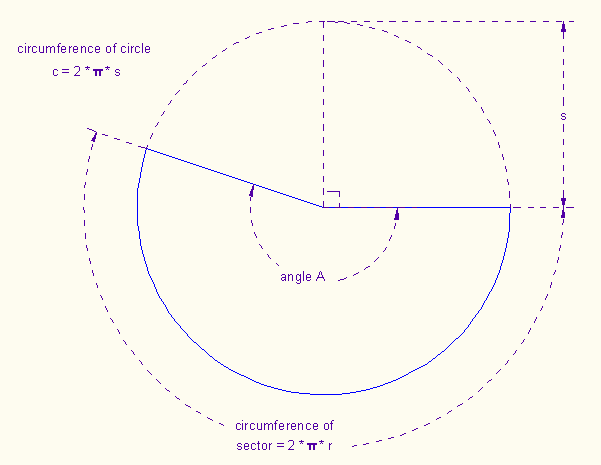
So angle A/360°= 2πr/2πs = r/s, and angle A = (r/s)*360°. Now we can design our cone!

Remark. A nice variant of this lesson is to make a larger cone out of a stiff transparency, and to make the smaller cone out of colored posterboard. The two pieces make a very attractive artifact!