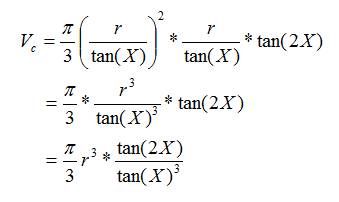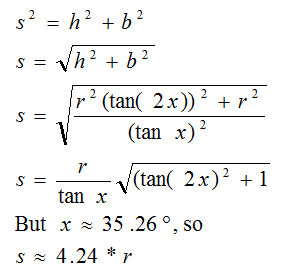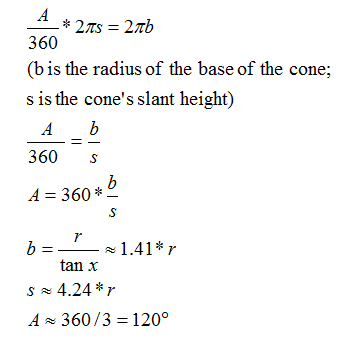Ball in a Cone

BallInConePhotoWithBoth.png

Task. Design and construct from poster board a cone that holds a golf ball. The cone should have its volume as small as possible.
What is the ratio of the volume of the ball to the volume of the cone?

Analysis.

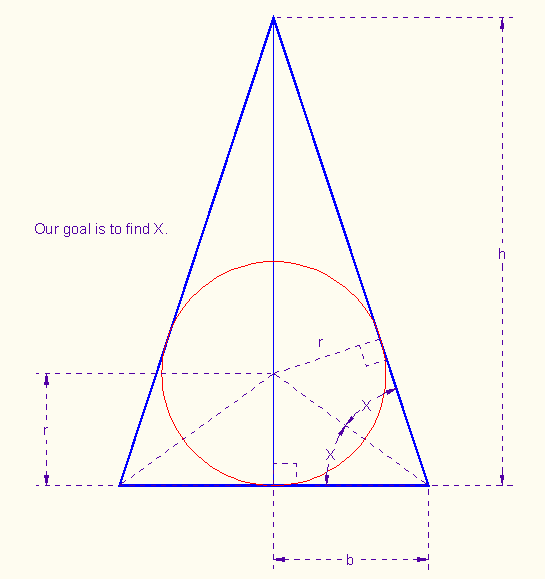
BallInConeCrossSection01.png

Vertical cross section of a cone with a sphere inside.

Naming variables:

b =

radius of base of cone (we don't know this)

r =

radius of ball (we measure this)

h =

height of cone (we don't know this)

X =

angle (also unknown; see diagram; if we find the value for X, we can find values for all other variables)

Then:
b = r / tan(X)
h = b * tan(2X)
We know that the volume of a cone = Vc = 1/3*(area of base)*height
And the area of a base with radius b = π*b2 = π*(r/tan(X))2
The cone's height h = b*tan(2X) = (r/tan(X))*tan(2X)

Substituting the values of b and h above in Vc, we have,
The volume Vc as a function of X and r is 1/3*(area of base)*height,

BallInConeEquation01.png

(Notice that π and r are constants.)

The minimum volume is reached for some value of X between 0 and 45 degrees. For this value, the derivative dVc/dX = 0.

Computation with the TI-83/84 Plus.

Set MODE to degrees.
Define,
\Y1=tan(2X)/tan(X)3 

(Or you may set \Y1=(π/3)*R3*tan(2X)/tan(X)3. If you do this, 
\Y2=nDeriv(Y1,X,X) be sure to store the golf ball's radius in R.) 

Set Solver to
Y2=0
X=30 (for example)
bound={0,45}
and ALPHA SOLVE.
You get X=35.26438965271.

From above, the values of b and h, in terms of r and X, are
b = r/tan(X) and h = r*tan(2*X)/tan(X)

The volume of the ball is Vb = 4/3*π*r3, and thus
Vb/Vc = 4*tan(X)3/tan(2*X).

Ratio of the volume of the ball to the volume of the cone:
4tan(X)3/tan(2X) ENTER returns .5. So the ball occupies exactly one half of the cone!

Design and construction.

Measure the diameter of the golf ball and compute its radius r. Follow the method of designing a cone of given dimensions described in Baggett & Ehrenfeucht, 2001. It is also included here.

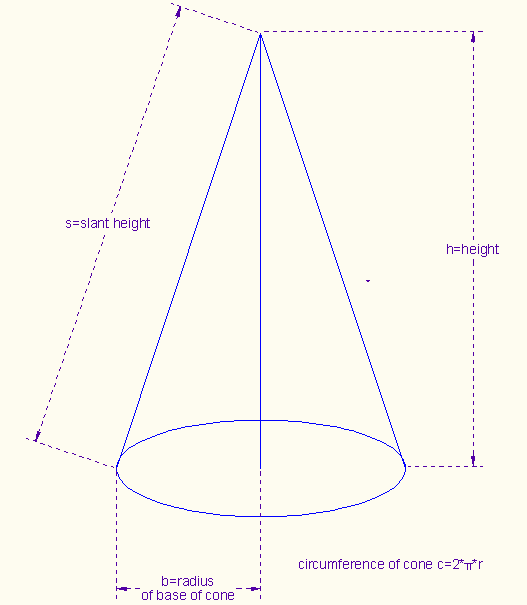
BallInCone3D.png

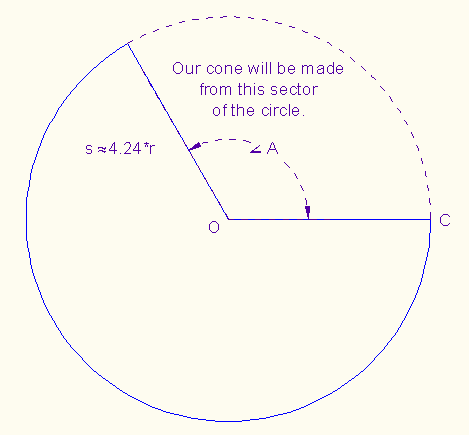
We use the Pythagorean theorem to find the slant height s.

BallInConeEquation02.png

BallInConeArcLength.png

Next we need to find angle A.

BallInConeEquation03.png

So we need a sector of A ≅ 120 degrees with radius s = 4.24*r, where r is the radius of the ball.

Warning.
The values that are computed describe the dimension of the interior of the cone. Because of the thickness of the poster board, the exterior of the cone must be slightly bigger. Otherwise the ball will not fit in.

Reference

Baggett, P. & Ehrenfeucht, A. (2001). Breaking away from the algebra and geometry book. Lahnam, MD: Rowman and Littlefield.

Webpage Maintained by Owen Ramsey
Calculus Index