Radians and Degrees
Measurements of
angles are based on the following theorem: In similar figures, corresponding
angles are equal.
Similarity of triangles can be used, for example, to measure the height of a
tree.
But because angles are preserved during rotation, it is therefore better to use
a circle instead of triangles or other polygons to measure angles.
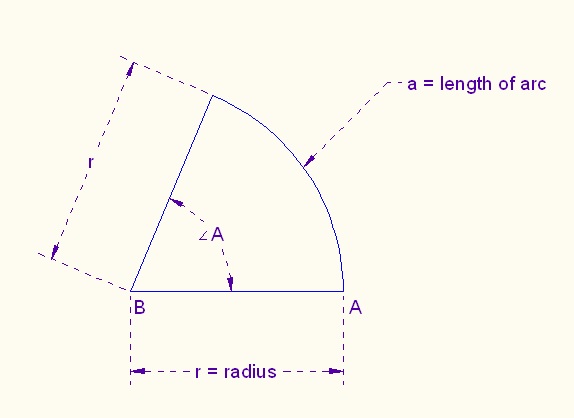
Consider a sector of a circle,
Take the ratio a/r
as a measure of angle A. This is the "most natural" measure of
angles, with the unit being the angle for which the length of arc a equals the
radius, namely, a = r. This unit is called a radian (from "an arc having
the length of a circle's radius").
But this definition has a serious drawback. What is the measure of a
right angle? It is 1/4*circumference/radius of a circle. But what is
this ratio, circumference/radius?
This last question happened to be difficult. (To know more about it,
read about the history of pi, for example, see Petr Beckmann's little book, History
of Pi (1970).) The methods of computing the ratio and
circumference/radius, that were accurate enough to make radians practical were
not developed until the seventeenth century.
Another way of measuring angles was invented in Babylon (which is at present located in northern Iraq) more than 3,500 years ago.
They first divided the circumference of a circle into 6 parts (this is
easy with a compass). Then they divided each part into 60 smaller
parts, which we now call degrees (they used base 60). When smaller
units were needed, they kept dividing each bigger unit by 60. So now
we have 1 degree = 60 minutes ("minute" means "small" in
Latin), and 1 minute = 60 seconds ("second small parts"). In
this way, the Babylonians bypassed the need for finding the ratio
circumference/radius.
The Babylonians' way of measuring angles was so successful that we still use
it. It even survived the introduction of the metric system, where
ratios of units are powers of 10 and not 60.
So why do we use radians at all?
In calculus, the most important concept is the rate of change (a derivative).
And the trigonometric functions sine, cosine, and others play a crucial
role in scientific applications of calculus.
Let's look at the following problem: y = sin(x). If x is measured in
degrees, the answer is (approximately),
|
|
dy/dx
= 0.0174532925*cos(x) (= 2π/360*cos(x)) |
(Not very pretty!)
But when x is measured in radians, the answer is exact,
|
|
dy/dx
= cos(x) |
And this is the reason
for using radians in most scientific calculations.
On the other hand, degrees are still preferred when actual measurements are
made.
Task 1.
Write one radian in degrees, minutes, and seconds.
Solution.
Set Mode to Degree.
Enter,
|
1r
|
|
|
|
|
ENTER
|
|
|
|
|
57.29577951
|
|
|
(You will find
radian, r, in 2nd ANGLE 3:r)
|
Ans►DMS
|
|
|
|
|
ENTER
|
|
|
|
|
57°
17' 44.806" |
|
|
(You convert to
degrees, minutes, and seconds with ►DMS in 2nd ANGLE 4: ►DMS)
Task 2.
Cut out a circle from poster board, or a large index card. Cut it
into 7 sectors. Six of them should have a central angle of 1 radian; the
remaining one is (approximately) 2/7 of a radian. Next, divide 1
radian (one sector) into these parts: 1/2, 1/4, 1/8, 1/8. Label all
the parts on one side with their measure in radians, and on the other side in
degrees and minutes.
Play with these pieces to become familiar with the meaning of one radian and
its parts.
Calculus Index