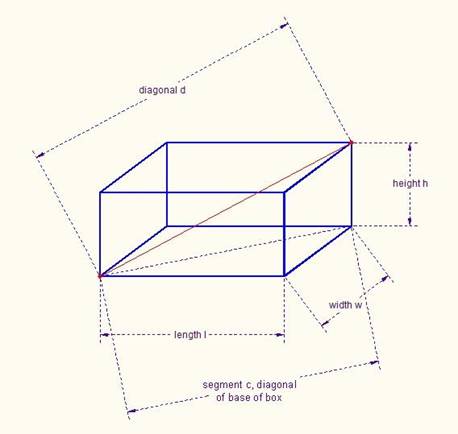
Diagonal of a Box
Suppose we have a
box with length, width, and height given, as indicated.
We want to know the
length of the diagonal d, shown in red on the diagram.
We can first compute the diagonal of the face of the box whose length l and
width w are given. Let's call this diagonal c.
c = √ (l2 + w2)
Notice that c is the leg of a new right triangle whose other leg is the height
h of the box, and whose diagonal d is the diagonal of the box. For
this right triangle, we know
d = √(c2 + h2)
But since c = √ (l2 + w2),
c2 = l2 + w2, so
d = √( l2 + w2 + h2)
And we have found how to get the length of the diagonal of a box with
dimensions l, w, and h!
Calculus Index