Normal
Distributions
A great variety of data can be represented by normal distributions. The reason is that when numerical outcomes of a process are determined by many mostly independent factors of equal importance, the resulting distribution is always very similar to the normal distribution. The main difference between the theoretical normal distribution and these observed distributions is that the theoretical distribution is defined for all real numbers, and observed frequencies always span a limited range of values.
The examples below were created on a TI-84 Plus C Silver Edition calculator, but you may use any TI-83 or TI-84 model. For the clearest picture, turn the axes off, and investigate the numerical properties of normal distributions using TRACE.
Example 1. Density distribution
Define and highlight:
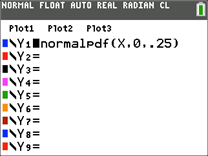
Set the window: Xmin=-1, Xmax=1, Ymin=0, Ymax=2, and GRAPH:
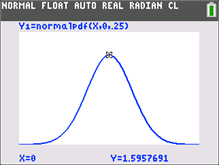
1. Investigate it with TRACE. Observe that the value for X=0 is Y=1.5957691. So the Y value does not show the probability of choosing a given value of X.
2. Edit Y1, replacing 0 and .25 by different values, for example, -2, and 3 (the second number must be positive); adjust the window, and again investigate it with TRACE.
Comments
(1) When you choose 2nd, DISTR, 1:normalpdf(, you see:
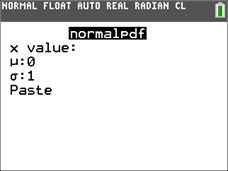
normalpdf stands for "normal probability distribution function";
μ is the mean value (mu) of the distribution, which is also the value of X for which the curve reaches its maximum;
σ is the standard deviation (sigma), which is a kind of theoretical unit used on the
x-axis.
(2) When we want to find the probability that the value of an outcome X is between two values A and B, A < X < B, we have to find the area below the curve Y1 and above the x-axis, between points A and B. We can do it in four different ways, which are described below.
Task
Find the probability that an outcome falls between A = -.5 and B= .1 in the normal distribution that has mean μ = 0, and standard deviation σ = .25.
First method
Graph the distribution as in Example 1. In 2nd, CALC choose 7:∫f(x)dx. You will see the prompt: Lower limit? Respond by entering, -.5. And to the prompt, Upper limit? respond by entering, .1. The area below the curve will be shaded, and below you will see:
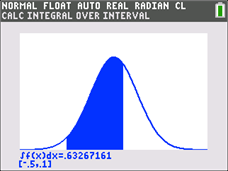
∫f(x)dx = .63267161
[-.5, .1]
which says that the required (theoretical) probability is .63... (around 63%).
Remarks
∫f(x)dx can be read "the area below the curve", but it also can be read: "The integral (elongated S) of a function f (here the function is Y1) relative to a variable x (here X)."
In order to find the probability for different values of A and B, enter 2nd, DRAW, 1:ClrDraw, to remove the shading, and repeat the same process.
Second method
You can do all the computations that are needed without graphing. Define Y1 as before. And then set MODE to CLASSIC:
choose MATH, 9:fnInt(, and compute:
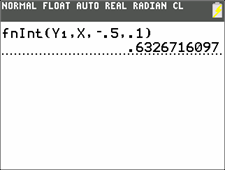
Remark
The computed formula can be read "The integral of Y1, computed for X changing from -.5 to ,1." Its value is the average value of function Y1(X), where X is changing from -.5 to .1, multiplied by the difference, .1 - -.5.
Example 2. Cumulative distribution
Third method
This method again requires graphing and some mental or paper and pencil computation. But this time you graph a cumulative normal distribution.
Define:
\Y2=normalcdf(-1E99,X,0,.25)
Set the window: Xmin=-1, Xmax=1, Ymin=0, Ymax=1, and GRAPH.
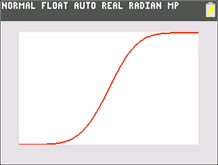
To compute the probability that the outcome falls between -.5 and .1: Find the value Y2(.1) and Y2(-.5), using 2nd, CALC, 1:value, or by using TRACE, and compute their difference.
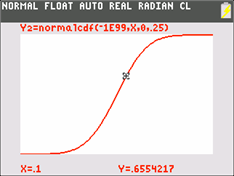
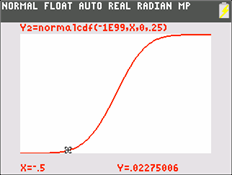
Fourth method
Define Y2 as before (in the third method above), and from the home screen, compute:

Comments
Theoretically the normal distribution is defined on all real numbers. But the TI-84 calculators handle only numbers between -1099 and 1099. So the smallest (negative) number for which the normal distribution can be computed is -1099 = -E99. So the cumulative distribution starts at -E99.
Lesson Index