
Task
Create a list of n numbers that are randomly chosen among the whole numbers from 1 to n. Guess how many different numbers are on your list. Check your guess. Repeat this action several times for different values of n. (Use as big an n as your calculator can handle without overflowing its memory. You should be able to handle lists up to 500 items.) Can you give a rule for making a “good guess”? Can such a rule be theoretically justified?
Plan of action and its execution
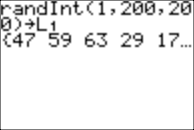
1. How to generate a list L1 of (for example) 200 numbers between 1 and 200?
randInt(1,200,200)→L1 ENTER
2. How to count the number of different items in L1?
SortA(L1):sum(0≠ΔList(L1))+1 ENTER
Remark
To understand this formula, create a short list L1, so you can see how many different numbers are on it. Then run your program in “piecemeal” fashion, looking at what happens during each step.
| L1 | ENTER |
| SortA(L1) | ENTER |
| ΔList(L1) | ENTER |
| 0 ≠ΔList(L1) | ENTER |
| sum(0≠ΔList(L1))+1 | ENTER |
3. Gather some data (an example)
N the length of the list of numbers chosen randomly between 1 and N;
D the number of different items on the list;
P = D/N presented as a percentage.
N: D: P:
100 62 62%
100 63 63%
200 131 66%
200 124 62%
… … …
Are you ready to make a prediction?
4. The theory behind these results
(a) The probability of missing a specific number, when you choose randomly one out of the numbers between 1 and n, is (n – 1)/n = 1 – 1/n.
(b) The probability of missing a specific number when you repeat such a choice n times is
(1 – 1/n)n.
(c) For reasonably big n, (1 – 1/n)n ≈ e-1 ≈ .3678794412
(d) Thus the expected value of the numbers missing from the list is approximately e-1*n,
and the expected value of the numbers occurring on the list is
n – e-1*n = (1 – e-1)*n ≈ .63*n.
So the ratio of D/N is often close to 63%, and all predictions slightly above 60% are reasonable.
****************************************************************************
Here is an example from the list in the screenshot above:
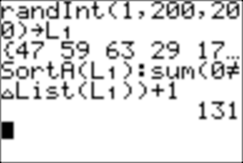
131/200 = .655