
Guessing game: Tossing one die
(At
the end of this unit, there is a TI-84 Plus C calculator simulation for playing
the game.)
One
die is tossed over and over again until each number from one to six shows up at
least once. Statistics are kept, and the total number of tosses needed is
recorded.
Before
play starts, all participants guess the total number of tosses. The lowest
reasonable guess is 6, but there is no upper limit.
If
you guess correctly, you earn 5 points; if you are one off, you earn 3 points;
if you are 2 off, you earn 2 points, and if you are 3 off, you earn 1 point.
Example.
you
toss: Mark on your score card:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
6 |
|
|
|
|
|
x |
|
5 |
|
|
|
|
x |
x |
|
5 |
|
|
|
|
xx |
x |
|
6 |
|
|
|
|
xx |
xx |
|
2 |
|
x |
|
|
xx |
xx |
|
1 |
x |
x |
|
|
xx |
xx |
|
1 |
xx |
x |
|
|
xx |
xx |
|
5 |
xx |
x |
|
|
xxx |
xx |
|
4 |
xx |
x |
|
x |
xxx |
xx |
|
2 |
xx |
xx |
|
x |
xxx |
xx |
|
3 |
xx |
xx |
x |
x |
xxx |
xx |
Thus,
after the game is over, the score card looks as follows:
| number on die: | 1 | 2 | 3 | 4 | 5 | 6 | |
| tally: | xx | xx | x | x | xxx | xx | |
| no. of times tossed: | 2 | 2 | 1 | 1 | 3 | 2 | Total = 11 |
So,
for example, guesses of 9 and 13 are two off, and each would earn 2 points.
Question.
What
is the mean value, m, of the number of tosses for this game?
Remark.
Students
must be told that mean value estimates the average that is computed from very
many examples. It is also called the "expected value", which is very
misleading, because in most situations we do not expect that any particular
result will match the mean or will even be close to the mean.
Finding
the mean.
Let’s
call a toss successful if it returns
a new value, and unsuccessful if it
returns a value seen before. So the game ends when we score 6 successful
tosses.
But
the probability of a successful toss depends on how many numbers have already
been seen. And this value varies from 0 at the beginning of the game to 5 when
only one number is left unseen.
| Number of numbers seen so far: | Probability of a successful toss: |
| 0 | 6/6 = 1 |
| 1 | 5/6 |
| 2 | 4/6 |
| 3 | 3/6 |
| 4 | 2/6 |
| 5 | 1/6 |
There
are two facts about probability that are needed to answer the original
question.
(1)
If the probability of success in one toss is p, then the mean value of the
number of tosses until the first success is 1/p (the reciprocal of the
probability of success).
Therefore
we have:
| Number of numbers seen so far: | Mean value of number of tosses until there is a successful one: |
| 0 | 6/6 = 1 |
| 1 | 6/5 = 1.2 |
| 2 | 6/4 = 1.5 |
| 3 | 6/3 = 2 |
| 4 | 6/2 = 3 |
| 5 | 6/1 = 6 |
(2)
The mean value of the sum of any random variables is the sum of their mean
values.
Here,
the number of tosses until the next success is one random variable. The first one is constant because the
success in the first toss is assured, but the remaining five are not.)
Therefore,
the mean value of the number of tosses until the game is finished is,
m = 1 + 1.2 + 1.5 + 2 + 3 + 6 = 14.7
tosses.
Remarks.
Of
course you do not expect 14.7 tosses in any game. The actual number of tosses
is a whole number. But you expect that the average over very many games would
be close to 14.7, provided that the die is not "loaded".
Three
to seven students sitting around one table can play one game. They should take
turns tossing a die, even if it is not relevant for the outcome.
Each
group has to keep score. They may compute the average of their games, but the
average of all games played in the class should also be computed. (The average
of all games can be different from the average of the averages from different
tables.)
Another
way to play the game, besides throwing a die, is to use the simulated program
ONEDIE shown below. We first give calculator screen dumps showing the program,
and then we give an example of a run. Finally, we give an explanation of the program code.
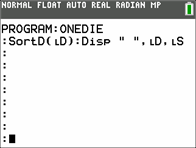
An
example of running the program





Let’s
see what the output means.
Roll
1 yielded a 2, and five other numbers (1, 3, 4, 5, and 6) were still needed.
Roll
2 yielded a 6, and four other numbers (1, 3, 4, and 5) were still needed.
Roll
3 yielded a 5, and three other numbers (1, 4, and 5) were still needed.
In roll
4, we got a second copy of 2, so the count of the number of twos was increased,
and the three other numbers, 1, 4, and 5 were still needed.
...
Roll
17 yielded a 3, so we are done. It took
17 rolls to get the numbers 1-6.
In
order from most to fewest, there were 5 twos and 5 sixes, 3 ones, 2 fives, 1
three, and 1 four that were rolled.
The “wait
times”, or numbers of rolls between new numbers, were 5, 4, 5, 1, and
1. So, for example, the third roll was a
five, and it took five more rolls to get the next new number, a 1.
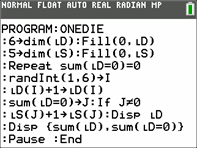
Program explanation.
|
PROGRAM:ONEDIE |
|
|
:6→dim(LD):Fill (0, LD) |
List
D holds the number of occurrences for each outcome. |
|
:5→dim(LS):Fill (0,LS) |
List
S is the five-element list shown at the end. It holds the
no. of times you wait for the next zero to be filled. |
|
:Repeat
sum(LD=0)=0 |
Repeat
the process below until the game ends. |
|
:randInt(1,6)→I |
A
random integer between 1 and 6 is stored in variable I. It
simulates a throw of a die. |
|
:LD(I)+1→LD(I) |
The
count of the Ith element in list D increases by 1. |
|
:sum(LD=0)→J |
The
no. of elements equal to zero in list D are put into J. |
|
: If J ≠0 :LS(J+1)→LS(J) |
Only
when J≠0, which indicates the game is not over, is
the corresponding element in list S increased by one. |
|
:Disp
LD :Disp {sum(LD), sum(LD=0)} |
List
D is displayed. Both the number of tosses so far, and
the count of how many new numbers are still needed,
are displayed. |
|
:Pause:End |
The
game ends. |
|
:SortD(LD); Disp " ",LD,
LS |
List
D is sorted, a blank line is inserted, and lists D
and S are displayed. |
Lesson Index