Displaying
Distributions:
Histograms, Cumulative Distributions
and their Inverses, and Percentiles
There are situations when you are not interested in the general properties of a distribution, such as the mean, the standard deviation, or even the probability of specific events. But instead, you are interested in the percentile ranking of a specific score, or in what score corresponds to a given percentile ranking. Some common examples are:
- when you want to know how your test score compares to the scores of the rest of the class, or
- when you want to know what score on the SAT exam would put you in the top 10% of all test takers.
In order to answer such questions, you may need two distributions.
One is the cumulative distribution of scores, in which, on the x-axis, there are scores, and on the y-axis is the probability (or frequency) that a score, S, is smaller than, or equal to, the value of x on the x-axis.
The other distribution is the inverse of the cumulative distribution. In such a distribution, the percentiles (cumulative frequencies) are on the x-axis, and the corresponding scores are on the y-axis.
Below we'll show how to construct both of these distributions, for a given list L of numerical outcomes, and how to use them.
Outline
Part 1. Cumulative distributions
Part 2. Displaying the histogram of an unsorted list and of a sorted list
Part 3. Displaying an inverse cumulative distribution
Part 4. Examples of (1), (2), and (3) above
Part 1. Cumulative distributions
To display a cumulative distribution on a TI-83/84:
Store the data from your list in L1. The list doesn't need to be sorted.
Define:
\Y1=sum(L1≤X)/dim(L1)
This function is defined for all X, not just for numbers in the range between min(L1) and max(L1), which covers all the numbers in list L1. The values of Y1 are between 0 and 1.
A reasonable setting of the WINDOW for graphing is,
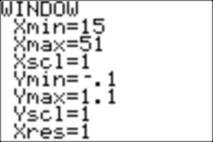
Xmin=min(L1), Xmax=max(L1)+1, Ymin=-.1, Ymax=1.1.
Now GRAPH. An example is in Part 4a below.)
Besides graphing, you may compute the percentile ranking of any score, or of a sequence of scores. (In the examples in Part 4 below, scores on the list vary from 15 to 50.)
(1) In order to get the percentile ranking of a score stored in variable S, compute:
100round(Y1(S),2) ENTER
Y1(S) is a decimal fraction. It is rounded to two decimal digits, and multiplied by 100, returning a percentile ranking.
(2) In order to get a ranking for several scores, for example, 37, 15.5, 41.86, and 46, compute:
100round(Y1({37,15.5,41.86,46}),2) ENTER
(3) You may compute the rankings of scores outside of the range of your list. The ranking of a score that is smaller than min(L1) is 0%. The ranking of a score higher than max(L1) is 100%.
Part 2. Displaying a histogram of a sorted list and of an unsorted list
The basic procedure that allows us to compute and graph the inverse of a cumulative distribution (where the percentiles (cumulative frequencies) are on the x-axis, and the corresponding scores are on the y-axis) begins with the "Display a list" (DISPLIST) program below (for the TI-83/84), which is the first step. DISPLIST creates a histogram for any list of numbers.
|
PROGRAM:DISPLIST |
|
|
:Input LL |
The program accepts a list of scores as input. |
|
:dim(LL)→D |
D is the dimension (i.e., the number of elements) in list L. |
|
:.6→Xmin |
This sets the graphing window a little wider than the |
|
:D+.4→Xmax |
range of the input list. |
|
:min(LL)→Ymin |
|
|
:max(LL)→Ymax |
|
|
:"LL(round(X,0))" |
This creates a function Y0 to be computed. The function |
|
→Y0 |
accepts any X with the range, and rounds it to the nearest |
|
:DispGraph |
integer. Finally, it graphs the function. |
Before running DISPLIST, you may sort your list in ascending or descending order, or you may leave it unsorted. (Of course this will result in different graphs.)
To run the program, turn off all functions Y, and turn off STAT PLOT. Start the program and at the ?, provide it with an input list. On the graph, you will see the numbers 1 through D along the x-axis, and you will see the scores stored in the list (in the order that they occur in the list) along the y-axis. From the home screen you may compute any value or any list of values of Y0(X), provided that X is within the range specified for the window. If X is out of the range, you will get an error message. (An example is given in Part 4 below.)
Part 3. The inverse of a cumulative distribution
To compute the inverse of a cumulative distribution, you must input a list of outcomes sorted in ascending order. Sorting the list is crucial here!
Then, edit the function Y0 that was created by the program DISPLIST:
\Y0= LL(round(1+.01X(D-1),0))
This computes the values on the x-axis so that they run from the zero percentile to the 100th percentile, and the y values go from the lowest score in the list to the highest.
Change the WINDOW setting: Xmin=-.4, Xmax=100.4
Now you may graph. (An example is given in 4d below.)
To compute the score for any percentile, P, between 0% and 100%, enter from the home screen:
Y0(P) ENTER
To compute the scores for a list of percentiles that you have stored in list LP, compute
Y0(LP) ENTER
Part 4a. An example of a cumulative distribution
We simulate scores from a test given to 67 people in which the number of points on the test varies between 15 and 50. We make our list L1 of 67 scores as follows (this will give us a distribution with more scores in the middle range; do you see why?):
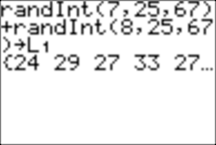
(Of course your data will be different!)
The values for Y will be cumulative frequencies varying from 0 to 1, so we set the window:
To get cumulative frequencies, we define (notice the xbefore Y1):
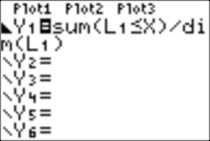
and we GRAPH:
On the x-axis, we have scores from 15 to 50, and on the y-axis, the range is from 0 to 1. We can use TRACE to look at scores (on the x-axis) and their percentile rankings as numbers between 0 and 1 (on the y-axis). Here, a score of 33 is at the 55.2th percentile, and a score of 45.25 is at the 94th percentile. This means that 55.2% of the scores are less than or equal to 33, and 45.25% of the scores are less than or equal to 94:
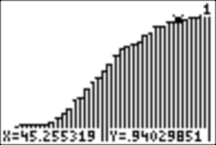
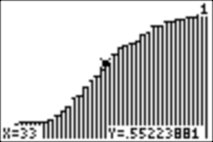
We can also find a specific percentile ranking of any score, S, from the home screen. (If we
enter Y1(42), we get, not a percentile, but an unrounded decimal between 0 and 1, as we did in the above graphs).

And we can get percentile rankings for several scores at once. Here, the scores are 25, 35, and 45:
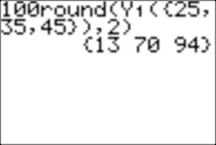
The meaning of these numbers: a score of 25 is at the 13th percentile; a score of 35 is at the 70th percentile; and a score of 45 is at the 94th percentile.
We can also compute the percentage of scores between two scores. For example, suppose we want to know the percentage of scores between 50 (the top score possible) and 40, between 40 and 30, and between 30 and 20, and between 20 and 15:
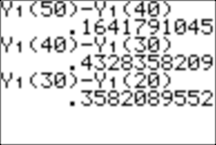

The bulk of the scores lie in the 30 to 40 range.
4b. Example of an unsorted histogram
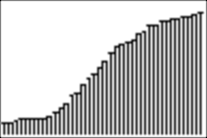
We run the program DISPLIST using our simulated test data presented above, using the unsorted list L1, and the result is:

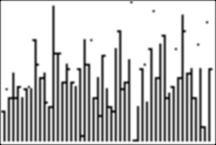
Using TRACE, we see that the first element in our unsorted list is a score of 24, and the second is 29. (But we already knew this from above!)
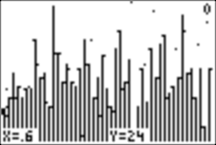
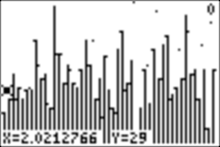
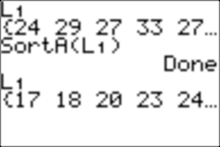
4c. Now let�s sort list L1 and graph a histogram with sorted data.

We explore it with trace:
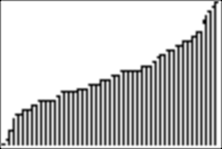
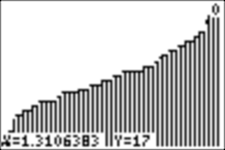
And for example, we see that the lowest score on the test, the first score, is 17.
4d. Our goal is to make an inverse cumulative distribution. We use the data from the example above, namely, test data with simulated scores ranging from 15 to 50, for 67 students; the data are stored in list L1).
The cumulative distribution will have percentiles from 0 to 100 along the X-axis, and scores from 15 to 50 along the Y-axis. Then we will be able to say, for example, what score(s) have a particular percentile associated with them.
We use list L1 which must be sorted from lowest to highest.
The program DISPLIST creates a function, Y0, which is put in the calculator. We edit Y0 so that it looks as follows (notice the x symbol before Y0=):
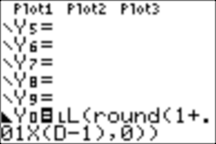
Next we set the window:
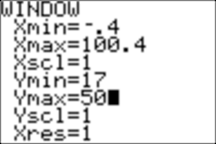
And
then we graph:
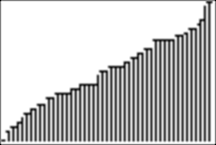
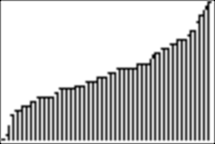
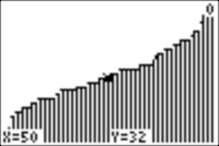
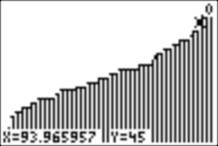
We can explore the graph with TRACE. Here, we see that a score of 33 (with 50 being a perfect score) is at the fiftieth percentile, and a score of 45 is almost at the 94th percentile:
We can use Y0 to get actual scores for any percentiles that we want. Here we ask for scores at percentiles 25, 50, 75, and 100:

And we can learn, for example, how many scores lie between the 80th and 90th percentile:

We
can use the information from our inverse cumulative distribution, for example,
to help in assigning grades to different scores.
Lesson Index