
The Birthday Problem
Here is one of the most popular applications of the laws of probability. There are many ways to set it up, but in any form it is always known as the birthday problem. Would you be willing to make an even-money bet that two children in a classroom with 26 children share the same birthday?
Setting aside the moral issue of wagering in front of children, we treat this as a scientific investigation and begin by asking each child his or her birthday. The first child's birthday might fall on any day of the year (we will ignore leap years and use a 365-day year). The probability that the second child's birthday is different is 364/365. Notice that we concentrate on the probability that there is NO match; this makes the problem easier.)
After the first child, there are 364 birthdays left that result in no match. After the second child, there are 363 days left, so the probability that the third child's birthday does not match either of the first two is 363/365.
Each of these events is independent of the others. Consequently, to find the probability that there are no matching birthdays among these three children, we multiply the probabilities:
(364/365)*(363/365) = 0.9918
So far, the chance of no matches is almost certain. But by the tenth child the probability of no matches is:
(364/365)*(363/365)(362/365)*(361/365)(360/365)*(359/365)(358/365)*(357/365) (356/365) = 0.8831
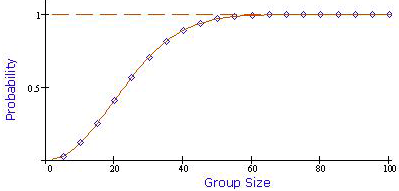
If we continue to the twentieth child, the probability of no match drops to 0.5886. The surprising result is that the fifty-fifty cutoff is at 23. If the group has 23 people, it is worth betting even money on two birthdays coinciding, because it has better than a 50% chance of being true. By the 26th child the probability of no match is down to 0.4018, which leaves close to a 60% chance of matching birthdays. In a classroom with 30 students, your odds of a match are better than 70%.
Suppose the group size is 25. The number of birthday possibilities is 36525. The number of these scenarios with NO birthdays the same is 365*364*363*...*342*341.
The number of cases having at least two birthdays the same is then:
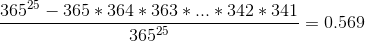
This argument can be generalized to a group of k people, giving the formula:
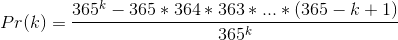
Using factorial (!) notation, this formula (for at least two birthdays) can be written as:
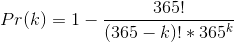
A graph of its growth behavior can be seen below.
So the formula for the probability that NO two people out of k people have the same birthday is:
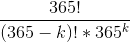
When we put this formula in our TI-83/84, we get an overflow error. But the formula can be written as: (365 nPr k)/365k.
nPr is the number of permutations of r out of n elements = n!/(n-r)!.
nPr is next to nCr in the probability menu.
For n = 365 and r = 23, the TI-84 gives 0.4927027657.
Why is the formula (365 nPr k)/365k correct?
Note that:
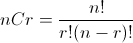
and
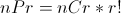
So
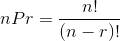
So
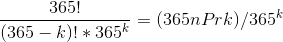
Calculator exercise for the TI-108
(by A. Ehrenfeucht)
What is the probability that in a classroom of 26 children, no two children share the same birthday?
Compute (364*363*...*340)/(36525)=
(364/365)*(363/365)(362/365)*(361/365)(360/365)*(359/365)(358/365)*(357/365)
(356/365)(355/365)*(354/365)(353/365)*(352/365)(351/365)*(350/365)(349/365)*(348/365
)(347/365)(346/365)*(345/365)(344/365)*(343/365)(342/365)*(341/365)(340/365)
Solution.
Keystrokes:
[365][M+]
For n = 340 up to 364, repeat,
[n][/][MRC][*]
(the last [*] may be replaced by [=])
Reason: (x1*x2* ...xk)/yk = (x1/y)*(x2/y)* ... *(xk/y)
Answer: The probability that no two of 26 children have the same birthday
is 0.4017577.