Part 1. Tossing two dice
Props: A pair of dice, a small cup, and a tally sheet
Toss two dice 36 times and record the outcomes on a tally sheet like this one; you may print one out below:
|
N u m b e r o f r o l l s |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
sum on two dice |
||||||||||||
|
Put an X in a square
(starting at the bottom) each time the sum on your 2 dice totals 2, 3, 4, 5,
6, 7, 8, 9, 10, 11, or 12 |
||||||||||||
Click here for a PDF copy of the above tally sheet!
From the tally sheet, do you see that some numbers come up more frequently than others? Which number(s) came up most frequently? Do you think this will always be the case? You may repeat the experiment using another tally sheet if you like.
It seems that the number 7 usually comes up much more frequently than 12. Why is this the case? Let's see in how many different ways we can get a score of 7, and in how many different ways we can get a score of 12. (It helps if the dice are different colors.)
First die: Second die: Sum:
1 6 7
2 5 7
3 4 7
4 3 7
5 2 7
6 1 7
First die: Second die: Sum:
6 6 12
There are 6 different ways we can get a score of 7, and only 1 way we can get a score of 12. So a score of 7 should come up more often.
Now compute in how many ways one can get each score between 2 and 12. Here is a chart:

Tallying these results, we have:
Score: Number of ways:
2 1 (1,1)
3 2 (1,2) (2,1)
4 3 (1,3) (2,2) (3,1)
5 4 (1,4) (2,3) (3,2) (4,1)
6 5 (1,5) (2,4) (3,3) (4,2) (5,1)
7 6 (1.6) (2,5) (3,4) (4,3) (5,2) (6,1)
8 5 (2,6) (3,5) (4,4) (5,3) (6,2)
9 4 (3,6) (4,5) (5,4) (6,3)
10 3 (4,6) (5,5) (6,4)
11 2 (5,6) (6,5)
12 1 (6,6)
Another way to look at these theoretical data:
Theoretical probability of the 11 outcomes from tossing two dice
|
outcome |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
frequency (fraction) |
1/36 |
1/18 |
1/12 |
1/9 |
5/36 |
1/6 |
5/36 |
1/9 |
1/12 |
1/18 |
1/36 |
|
frequency (decimal) |
.0278 |
.0556 |
.0833 |
.1111 |
.1389 |
.1667 |
.1389 |
.1111 |
.0833 |
.0556 |
.0278 |
And we can put the theoretical probabilities into a frequency distribution:
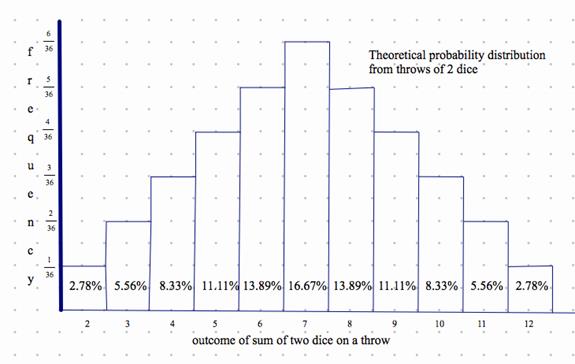
So we may think that if we throw the dice many times, then we will see a score of 7 most often; next (not so often, but still often) we will see scores 6 and 8; next 5 and 9; next 4 and 10; next 3 and 11; and least often 2 and 12. Does it really happen as we may think? No! Not necessarily! What happened when you tossed your dice above?
Remark.
It is possible (although not likely in the case of honest dice) that something very unusual will happen. (For example, 12 can occur more often than 7.) In such a case the experiment should be repeated again, and the word "usually" should be used. Around 50 throws in one experiment should be enough to observe the phenomena discussed above.
Return