Survivor on a Hexagonal Island

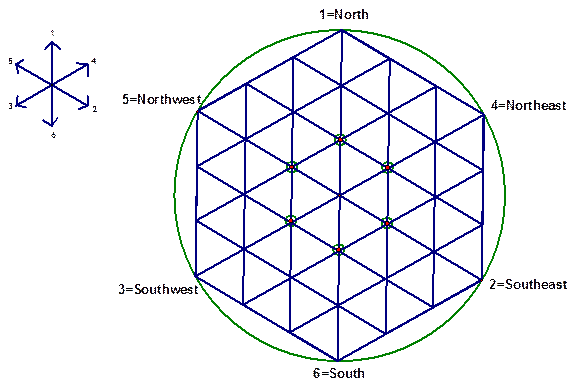
AKA Random Walk

First task.  Design the board above on poster board or paper or card stock.  It should be rather large--start with a circle with radius 9 cm.  The side of a "small triangle" should be 3 cm long. (It is better than 1 inch.)  The six directions should be indicated by arrows in the six corners of a big hexagon and marked with the numbers 1 to 6. A good pairing of opposite directions is (1, 6), (2, 5), and (3, 4), the same as on a die.

We recommend that you then color-code the paths on the island according to this map:

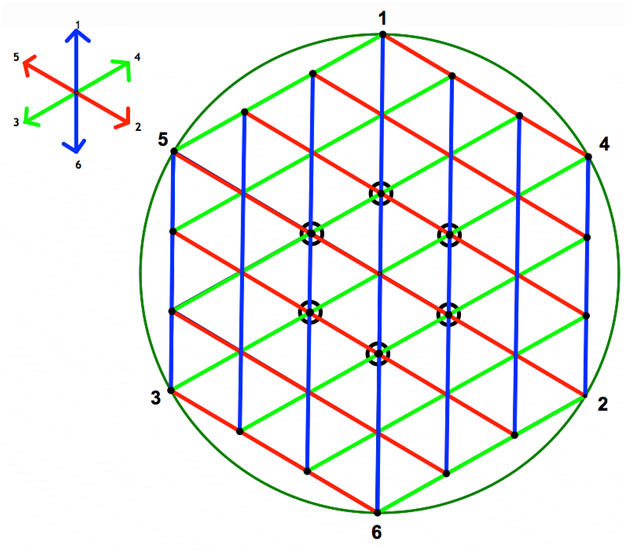
blue is North to South
red is Northwest to Southeast
green is Northeast to Southwest

These colored paths will help when you play the game.

Second task.  The game.
Two to six players play on one board.  Each person has a different color token (a penny, a colored plastic disc, etc.)  Players choose initial positions on the board, which can be any of the six vertices closest to the center of the circle (above they are marked with small circles), and place their tokens on their chosen position.

Players begin by rolling one die, and the person with the lowest number plays first.  Play proceeds clockwise.
Players roll one die at each turn.  The number on the die tells the direction that the token moves: up (1, on the blue path), down (6, on the blue path), northeast (4, on the green path), southwest (3, on the green path), northwest (5, on the red path), southeast (2, on the red path). A token makes a one-step move in the specified direction.  You stay on the island until the die roll forces you to leave.
The object of the game is to be the last one to leave the island.

You may add this condition to the rules:  If you move on a position occupied by another player’s piece, his/her piece is out and he/she loses. (This makes the game faster and more interesting.)  

Survivors are ranked in order of their leaving the board (falling into the ocean).
A LONGER stay on the board is better. We call it “Survivor on a Hexagonal Island".

(3) The program in the next unit does some computations that are summarized here. The expected time to exit the board by a single player starting in "basic position" (the mean number of moves) is 12 (the median number of moves is 9), so the game is not very fast. Here is a table of the cumulative probabilities of getting into the ocean by move number N (for example, by move 11, there is a 61% chance that one has left the island, and after move 11, theoretically there is a 5% greater chance (61% - 56%) that one will leave the island):

*12 is the expected value (the mean value) at the very end
**9 is the median value
So you may have very long-living survivors.  We suggest an extra rule: When more than one person survives, for example, 40 moves, the game is a draw.