A TI-84 program that a gives a theoretical analysis of
Survivor on a Hexagonal Island

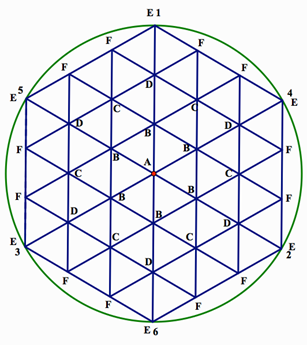
The program ISLAND uses the table below, whose letters correspond to positions on the hexagonal island picture above. The fractions in the table are the probabilities that from a given position one will get to another position. For example, from position B, the probability that you will move to position C is 1/3, since from B a move takes you to A, B, C, D, C, or B.
start targets
| L2(1) | L2(2) | L2(3) | L2(4) | L2(5) | L2(6) | |||
|
|
A |
B |
C |
D |
E |
F |
exit |
sum |
|
L1(1)=A |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
L1(2)=B |
1/6 |
1/3 |
1/3 |
1/6 |
0 |
0 |
0 |
1 |
|
L1(3)=C |
0 |
1/3 |
0 |
1/3 |
0 |
1/3 |
0 |
1 |
|
L1(4)=D |
0 |
1/6 |
1/3 |
0 |
1/6 |
1/3 |
0 |
1 |
|
L1(5)=E |
0 |
0 |
0 |
1/6 |
0 |
1/3 |
1/2 |
1 |
|
L1(6)=F |
0 |
0 |
1/6 |
1/6 |
1/6 |
1/6 |
1/3 |
1 |
|
PROGRAM:ISLAND |
|
|
:{0,1,0,0,0,0}→L1 |
1 represents the initial position of a player (position B on the island). |
|
:{0}→ L2 |
L2 is filled with zeroes; it is currently empty. |
|
:0→E |
E for Exit is the cumulative probability of getting off the island. It starts at 0. |
|
:0→N |
N is the number of the step. |
|
:0→A |
A is the current average no. of steps to exit the island. |
|
:While N≤ 2000 |
The program stops if N is greater than 2000. (You may modify this.) |
|
:N+1→N |
Increase the step number by 1. |
|
:6-1 L1(2) →L2(1) |
The value for L2(1) comes from column 1 of the table. |
|
:L1(1)+3-1L1(2)+3-1L1(3)+ 6-1L1(4) →L2(2) |
The value for L2(2) comes from column 2 of the table. |
|
:3-1L1(2)+ 3-1L1(4)+ 6-1 L1(6)→L2(3) |
The value for L2(3) comes from column 3 of the table. |
|
: 6-1L1(2)+ 3-1L1(3)+ 6-1 L1(5)+6-1L1(6)→L2(4) |
The value for L2(4) comes from column 4 of the table. |
|
: 6-1L1(4)+ 6-1L1(6)→L2(5) |
The value for L2(5) comes from column 5 of the table. |
|
: 3-1L1(3)+ 3-1L1(4)+ 3-1 L1(5)+6-1L1(6)→L2(6) |
The value for L2(6) comes from column 6 of the table. |
|
: 2-1L1(5)+ 3-1L1(6)→D |
The value for D comes from column 7 (exit) of the table. It is the probability of leaving the island at the current step. |
|
:E+D→E |
E is the cumulative probability of leaving the island. |
|
:L2→L1 |
The new distribution becomes the old distribution for the next step. |
|
:A+ND→A |
The mean value of the number of steps A to leave the island is updated. |
|
:”END” |
“END” is blocked |
|
:Disp round({N,A,E},3) |
Display the number of steps N, the average number of steps, and the cumulative probability of leaving the island, rounded to 3 digits. |
|
:Pause :End |
If “END” is unblocked, the program continues to 2000 steps and will show the results. Look at L1. It will equal {0,0,0,0,0,0} |
Here is some output from the program:
{1 0 0}
{2 0 0}
{3 .208 .069} On the 3rd move, 6.9% of players end up in the ocean.
{4 .517 .147} On the 4th move, 14.7%-6.9%=7.8% more end up in the
ocean.
{5 .927 .229} On the 5th move, 22.9% - 14.7% = 8.2% more end up in the
ocean.
{6 1.396 .307} On the 6th move, 30.7% - 22.9%=7.8% more end up in the
ocean.
…
{49 11.703 .995}
{50 11.730 .995} On the 50th move, less than .09% more end up in the
ocean.
…
To compute the middle numbers in the list above:
On step 3, 6.9% have made 3 moves to exit, for a total of .069*3= .207
moves (rounded).
This is the average number of moves it has taken everyone thus
far to leave the island.
On step 4, 7.8% have made 4 moves to exit, so the total moves to leave now
is (.078*4)+(.069*3)= .519
This is the average number of moves it has taken everyone thus
far to leave the island.
On step 5, 8.2% have made 5 moves to exit, so the total moves to leave now
is (.082*5)+ (.078*4)+(.069*3)=.929, the average number of moves it has
taken everyone thus far to leave.
Can you figure out the middle number for step six?
Notice that the middle number (above, after 50 moves, it is 11.730) is
getting closer and closer to 12. So the average number of moves for
everyone to leave the island is closer and closer to 12.