More about the Mode
The program MODE accepts a list of numbers and returns the number that is the mode of the list, when there is just one number that occurs more times than any other. Otherwise it gives the message "NO MODE".
We first show how the program looks on the calculator screen, and then we give an explanation of each line of code.

|
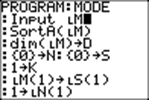
PROGRAM:MODE |
|
|
:Input LM |
The input list is read |
|
:SortA(LM) |
and sorted in increasing order. |
|
:dim(LM)→D |
|
|
:{0}→N:{0}→S |
Lists LN and LS are created and initialized. |
|
:1→K |
List S holds the set of all different outcomes from list M, |
|
: LM(1) →LS(1) |
sorted in increasing order. And list N holds the |
|
:1→ LN(1) |
number of occurrences of each outcome. |
|
:For (I,2,D) |
|
|
:If LM(I) = LS(K) |
List M is scanned. When an outcome is already on list S, |
|
:Then |
the number of occurrences, kept on list N, |
|
: LN(K) +1→LN(K) |
is increased by 1. |
|
:Else |
When a new outcome is found, it is put on list S, |
|
:K+1→K |
and one is put on list N. |
|
: LM(I)→LS(K) |
|
|
:1→LN(1) |
|
|
:End:End |
|
|
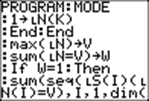
:max(LN)→V |
V is the biggest number of occurrences recorded in N. |
|
:sum(LN=V)→W |
W is the number of different outcomes occurring V times. |
|
:If W=1:Then |
When W=1, we have the unique mode. |
|
:sum(seq(LS(I) LN(I))=V),I,1,dim(LS))→M |
When W>1, no outcome is the mode. When there is a unique mode, it is stored in M. |
|
:End |
|
|
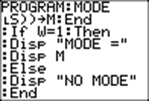
:If W=1:Then |
|
|
:Disp "MODE=" |
Either M or the message "NO MODE" is displayed. |
|
:Disp M |
|
|
:Else |
|
|
:Disp "NO MODE" |
|
|
:End |
|
After the program stops, you may view any of its lists and variables:
LM is the list whose mode you want to find.
LS lists all the different outcomes of list M.
LN holds the number of occurrences of each outcome.
V is the biggest number of occurrences in list N.
W is the number of different outcomes, namely, the dimension of list S.
D is the number of outcomes in the original list M, namely, the dimension of M.
If you put lists S and N as Xlist and Freq in STAT PLOT and set the window variables right, you can graph the distribution of outcomes from your input list.
A good setting of the window:
Xmin must be smaller than or equal to LS(1) and
Xmax must be greater than LS(dim(LS)).
The range of Y cannot be smaller than from 0 to max(LN).
A simple example of how to use the program MODE and how to display the data.
Suppose we want the program to tell us the mode in this list:
{1,2,3,4,2,4,4}
We run the program and enter the list:

It tells which number is the mode:

You can ask it to display three lists, LM, LS, and LN:
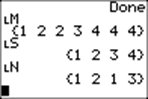
LM is the original list, which is now ordered.
LS gives the four different numbers that occur in the list.
LN tells the number of occurrences of each of the four different numbers, in order.
You can also ask for the values of three variables, V, W, and D.

V is the largest number of occurrences of a member of the list (here, there are 3 fours).
W is the number of different outcomes that occur V times (here, there is only one).
D is the number of elements in our original list M.
Now we can plot the number of occurrences of each element of the list by using STAT PLOT. We set Xlist to S, and Freq to N:
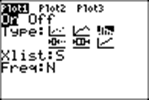
We set the window as above:

And we get a graph, which we can examine with TRACE:
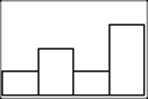
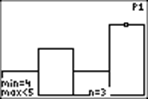
Task.
Simulate 30 tosses of two dice, and save the results in list M. Do you think that the mode of your list will be 7? Enter the program MODE into your calculator, and run it and see!
After running the program, look at lists M, S, and N, and at the values of variables V, W, and D, and interpret them.
Then set the calculator window appropriately, and run Stat Plot, setting Xlist to be S and Freq to be N. Now graph your histogram and explore it with TRACE.
Finally, find the mean, median, and first and third quartiles of list M using STAT CALC and 1-Var Stats. (Remember that 1-Var Stats does not find the mode!)
Lesson Index