Mini Slot
Machine
Gambling
is mostly a losing game. The most popular games in casinos are slot machines.
Modern slot machines are electronically controlled; the spinning wheels,
sounds, and other props are only window dressing.
In
this unit we implement and play with a mini-slot-machine. You may pretend that
you are playing for pennies, or if you are a gambler you may imagine that you
are playing for dollars.
The probability of the payoff (for a 1¢ play) are:
| payoff: | 0 | 1 | 2 | 10 (the jackpot) |
| probability: | .65 | .2 | .1 | .05 |
So
the average return for 10¢ is 9¢ (the payoff for 1¢ is.65*0 + .2*1 + .1*2 +
.05*10 = .9, and the payoff for 10¢ is ten times more, or 9¢). This means
that the expected profit rate for the "casino" is 10% per play.
In real casinos you sometimes know the rate of profit, but you are never told
the actual distribution.
Task 1.
Design a program for the TI-84 that generates the values 0, 1, 2, and 10, with
the probabilities .65, .2, .1, and .05
The
key point is to create a step function, f:
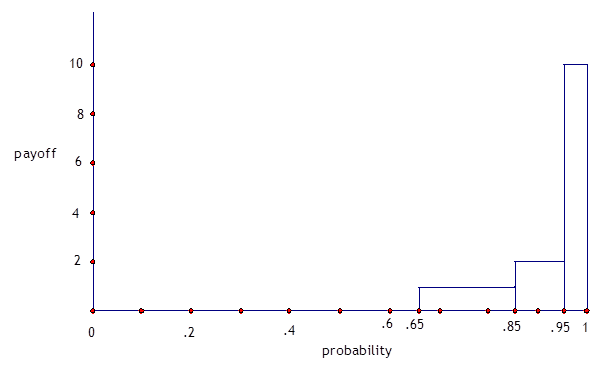
This
function f returns:
f(x) = 0, for 0 ≤
x < .65;
f(x) = 1, for .65 ≤
x < .85
f(x) = 2, for .85 ≤
x < .95
f(x) = 10, for .95 ≤
x < 1.
Now
if we compute f(RAND), where RAND returns values
between 0 and 1 with uniform probability, we get:
0
with probability .65,
1
with probability .85-.65 = .2,
2
with probability .95-.85 = .1, and
10 with probability 1-.95 = .05.
Implementation:
|
:PROGRAM:MINISLOT |
|
|
:0→N |
N
counts the number of bets, i.e., the amount you bet, one unit (penny or
dollar or ...) per trial |
|
:0→T |
T is
the total amount you have won so far |
|
:While
1 |
|
|
:RAND |
|
|
:iPart(Ans+.35)+ |
|
|
iPart(Ans+.15)+8 |
|
|
iPart(Ans+.05)→P |
P
is the amount (payout) you win on this trial |
|
:N+1→N |
|
|
:T+P→T |
|
|
:Disp{N,P,T} |
|
|
:Pause |
|
|
:End |
|
Explanation.
1 -
.65 = .35 is the probability that the payoff is bigger than 0.
So
if Ans ≥ 0.65, then iPart(Ans
+ .35) = 1.
In
addition, if Ans ≥ 0.85, then iPart(Ans + .15) is also 1.
And
if in addition, Ans ≥ 0.95, then 8*iPart(Ans + .05) equals 8.
So
payoffs of 0, 1, 2, and 10 are generated with the probabilities .65, .2, .1,
and .05.
Remarks.
Study
P carefully in order to see that for values x between 0 and 1 it computes
f(x).
Run
the implementation of a mini-slot-machine, prgmMINISLOT.
Task
2.
Students work in groups of 4. Each student starts with 20 pennies. One
student is the "cashier" (who gets 20 extra pennies) and keeps
pennies on a paper plate. The remaining three students are "gamblers".
A gambler pays a penny to the cashier and "plays" the
calculator. If he/she wins, the "cashier" pays out the
winnings.
The game ends when a "gambler" decides to quit, or loses all the
money, or the total time allotted for the game by the teacher (for example 10
minutes) runs out.
All students (including the cashiers) record their winnings or losses.
After
the game is played a few times, students discuss their strategies and the
outcomes.
Lesson Index