Mode, mean, median, and quartiles

 

You do not need to think about probability to learn about the concepts in this unit; you only need to think of making sense out of a list of numerical data. hen you think about probabilities, you often consider infinite sets of data, such as all whole numbers or all real numbers, which we avoid in this unit.

 

Each of the numbers mode, mean, median, and quartile answers a specific question.

Which value occurs most often?

If there is one such value, it is the MODE. If there are many, you need to hedge, or list all of them.

What is the average of all the numbers?

For every finite list there is such a number; it is the MEAN. For infinite sets of data the mean may not exist.

You want to order the data by size and divide them into two groups of equal, or almost equal, size. The question is, where do you make a cut?

It is answered by the MEDIAN.

When you want to put data into four bins, you also need QUARTILES.

 

Task

Choose two numbers, for example, 10 and 20. Make a random list of length 20 of numbers from 1 to 10 and store them in list L1. Here is an example:

You may sort it and look at the sorted list L1 on the home screen:

 

And you may scroll through to see all the values,

2 3 4 4 4 5 6 6 6 7 7 7 8 8 9 9 10 10 10 10

 

Find the values of mode, mean, and median of your list by hand.

 

Move to STAT CALC and choose 1:

 

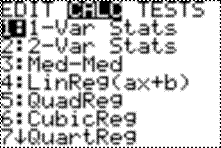
After you press enter you will see

1-Var Stats

And you enter L1:

 

and press ENTER. You will see

 

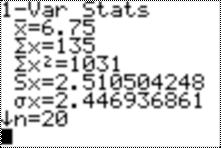
You can then see that

 

image014= 6.75

mean

minX=2

 

Q1=4.5

first quartile

Med=7

median

Q3=9

third quartile

maxX=10

 

 

In the example here, the mode is 10, but it is not a part of STAT CALC.

(Other statistics are also computed by STAT CALC: sum of squares of the numbers, the sample standard deviation and the population standard deviation. We will talk about them in another lesson.)

Webpage Maintained by Owen Ramsey
Lesson Index