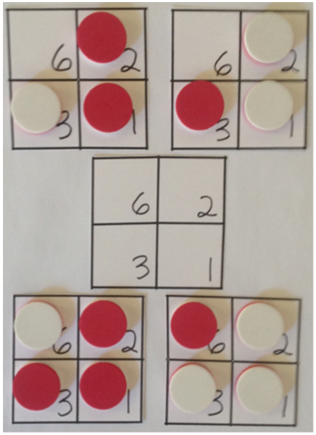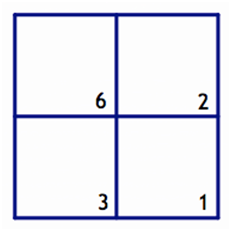
Ways to make the numbers zero through 12 on the 2 by 2 board above using at most one token per square (A white token signifies a positive number, and a red token signifies a negative number.)

Supplies: Four two-color tokens and a board
A list of the ways to make zero through twelve:
| 0 | = | 3-2-1 | 6-3-2-1 | 1+2-3 | 3+2+1-6 | empty board | 5 ways |
| 1 | = | 1 | 2-1 | 3-2 | 6-3-2 | 4 ways | |
| 2 | = | 2 | 3-1 | 6-3-1 | 3+1-2 | 6+1-3-2 | 5 ways |
| 3 | = | 3 | 1+2 | 6-3 | 6-2-1 | 4 | |
| 4 | = | 3+1 | 3+2-1 | 6-2 | 6+1-3 | 6+2-3-1 | 5 |
| 5 | = | 3+2 | 6-1 | 6+1-2 | 6+2-3 | 4 | |
| 6 | = | 6 | 1+2+3 | 6+1+2-3 | 6+3-1-2 | 4 | |
| 7 | = | 6+1 | 6+2-1 | 6+3-2 | 3 | ||
| 8 | = | 6+2 | 6+3-1 | 6+3+1-2 | 3 | ||
| 9 | = | 6+3 | 6+2+1 | 2 | |||
| 10 | = | 6+3+1 | 6+2+3-1 | 2 | |||
| 11 | = | 6+2+3 | 1 | ||||
| 12 | = | 6+1+2+3 | 1__ | ||||
| 38 ways |
How do we know we have them all?
On each of the four squares, there can be "no token," a white token, or a red token. So for each square there are 3 possibilities. 3*3*3*3 = 81, so there are 81 possible configurations of tokens.
As listed above (and shown below!), 5 of them make zero, so 81-5 = 76 are not zero. 76/2 = 38 are positive, and 38 are negative. The 38 positive configurations are listed above.
Postscript.
Here are the five ways to make zero: