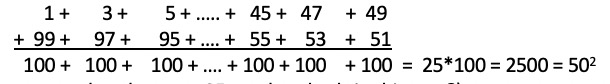A story about the German mathematician Karl Friedrich Gauss (1777-1855) during his early school years goes like this. The teacher wanted to keep the class busy, so he (the teacher was male) told students to add up the whole numbers from 1 to 100. But after a few minutes young Gauss presented the following answer: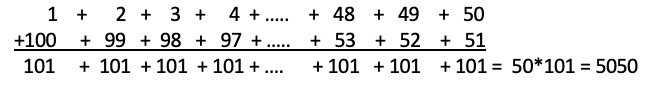

A general formula, which is true for all whole numbers n, which are either even or odd, is

This method is more than just a clever trick. It is used in many problems involving sums. You try to rearrange the computation of a sum so that many additions can be replaced by one multiplication.

Using the formula, can you compute the sum of the whole numbers from one to ten?

As a slightly different example, consider this problem:       Add all the odd whole numbers from one to 99. Again, rearrange the computation as previously: (Do you see that there are 25 one hundreds in this sum?) A general formula for the first (2*n – 1) odd numbers is 1 + 3 + 5 + …. + (2*n-3) + (2*n -1) = n2.

Short animation about the sum of the first n odd numbers. https://www.youtube.com/watch?v=IJ0EQCkJCTc

Can you compute the sum of the even numbers from zero to one hundred?

Here is a tricky one. What about the multiples of 3 from 3 to 99? (Notice that the number of terms in this sum is odd.)

This technique can be used for computing the sum of the consecutive terms of any arithmetic progression. An arithmetic progression is a sequence of numbers such that the difference of two consecutive terms is a constant. So 1, 2, 3, 4, …. is an arithmetic progression. So is 1, 3, 5, 7, …. And so is 2, 4, 6, 8, 10, 12, and so is 7, 13, 19, 25, and so is 1.5, 3, 4.5, 6, 7.5, 9, and so is -3, 0, 3, 6, 9, 12, and so is .75, 1.5, 2.25, 3, 3.75.

If a₁, a₂, a₃, …….., a_n is any arithmetic progression, then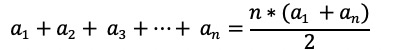

Here, the numbers a₁, a₂, a₃, …….., a_n and their differences do not have to be whole numbers, or even positive numbers.

Make up your own arithmetic progression, and see if you can sum it using the formula!