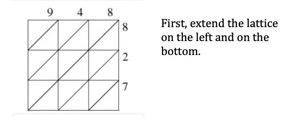
Lattice Multiplication
|
In this unit we will learn a method for performing multiplication of whole numbers that was used in the past. It has been used historically in many different cultures. According to Wikipedia, it is not known where it arose first, nor whether it developed independently in more than one region of the world. It can be found in early Arabic, European, and Chinese mathematics. David Eugene Smith, an American mathematics education historian, asserted that it was brought to Italy from the Middle East. The Italian term for the method is gelosia, namely, the metal grille or grating (lattice) for a window. The method is more visual than the method we use today, and it is currently often taught in schools. 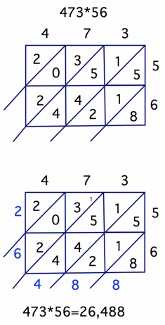
Draw vertical lines, one more than the combined number of digits in the two numbers. Next, draw horizontal lines, one more than the number of digits in the second number. You now have a grid of squares. Draw the diagonal lines so that your squares are cut in half. Place the digits of the first number across the top and the digits of the second number down the right hand side. Each pair of digits, one from each number, corresponds to a square made up of two triangles. Multiply each pair of digits, placing the result in the two triangles. To get the product of the two numbers, add the numbers in each slanted column, carrying digits, if necessary. The product will then be at the bottom of the lattice. Here is another way to look at 473*56: 
Can you find the six products shown with this method in the lattice above? Do you see how the lattice takes care of multiplying by 1, 10, and 100? 
Go vertically and horizontally from where the two decimal points originate, until the two lines intersect. From there, go down a diagonal until you get to the answer. (See the red lines above.) Problems. Use the lattice method to work the following multiplications.
There are many other multiplication algorithms. One is called Russian Peasant Multiplication, http://mathforum.org/dr.math/faq/faq.peasant.html. Another is the Egyptian method, http://mathforum.org/library/drmath/view/57542.html. Lesson Index |