Mathematical Kites

[Note to the reader:

In this unit we call all quadrilaterals kites. This is not the standard definition of a kite. Usually a kite is described as a special kind of quadrilateral, but the exact definitions often vary. The most general definition that is typically used: A kite is a quadrilateral in which one of its diagonals is its axis of symmetry. This definition is equivalent to the following one: A kite is quadrilateral that has two pairs of equal adjacent sides. These two definitions include rhombuses and non-convex quadrilaterals. Other definitions of kites are narrower. Sometimes only convex quadrilaterals are called kites and non-convex ones are called arrowheads. Sometimes rhombuses are excluded by the additional condition that not all sides are of equal length.]

A quadrilateral, also called a kite, is a polygon that has four sides. In order to form four corners of a kite, four points on the plane must be "independent". This means that no three of them are on the same straight line.

But four corners do not always determine a kite in a single unique way.

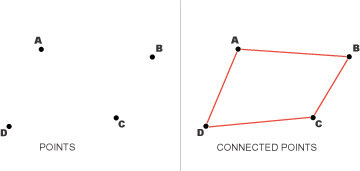In figure 1 there is only one possible kite with these corners. Its sides are:
AB, BC, CD and DA

and it is a convex polygon.

Figure 1

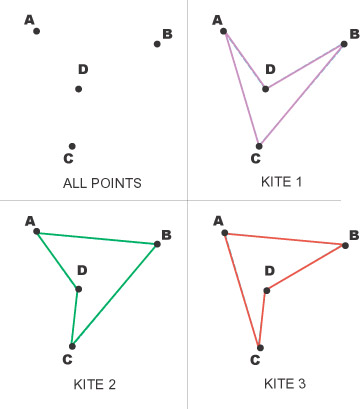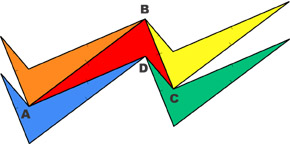
In figure 2 there are three possible kites with these corners. Their sides are:
Kite 1: AD, DB, BC and CA;

Kite 2: AB, BC, CD and DA;

Kite 3: AB, BD, DC and CA.

None of them is convex.

Figure 2

Every kite has two diagonals.

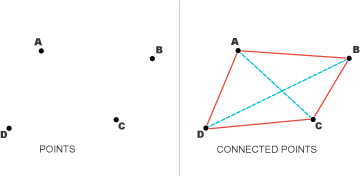In figure 3, the diagonals, shown as dotted blue lines, are
AC and BD.

Figure 3

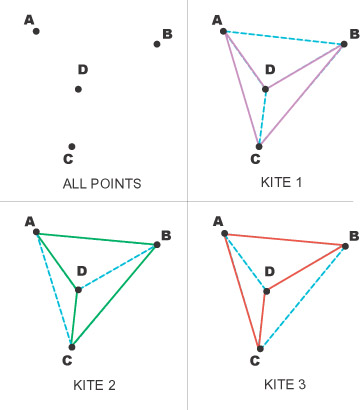In figure 4, the diagonals, shown as dotted blue lines, are respectively,
Kite 1: AB and CD

Kite 2: AC and BD

Kite 3: AD and BC.

Figure 4

In convex kites, the diagonals intersect; in concave (not convex) kites, they do not.

Every diagonal is shorter than 1/2 of the perimeter. For example, in figure 3,

|AC| < |AB| + |BC|, and |AC| < |CD| + |DA|,

by the triangle inequality. Therefore:

|AC| < ( |AB| + |BC| + |CD| + |DA| )/2.

In addition, in every convex kite, the sum of the diagonals is longer than 1/2 of the perimeter. (Can you prove it?)

Every kite can be decomposed into two triangles. So the sum of the angles of a kite is 360 degrees.

It is easy to see that every rectangle tessellates the plane. Less obvious but true is a more general fact that every kite tessellates the plane. (Some of these tessellations are quite interesting.)

Activity:
We will use kites to tessellate the plane. In order to cover the plane, you will rotate each kite 180° around the middle point of each of its sides. Such rotations fill the whole plane with copies of the kite. The picture at the top of this page is an example. Print out and color several identical kites using the printable page below. (Or design your own!) To get your started, we included some pictures.

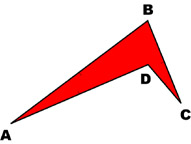Kite ABCD

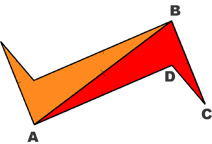Rotate ABCD 180° around the middle point of AB

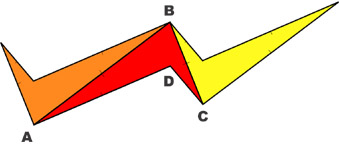Rotate ABCD 180° around middle point of BC

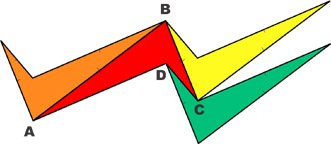Rotate ABCD 180° around middle point of CD

Rotate ABCD 180° around middle point AD.

Notice that the four different vertices of the kite always meet at a point. Here we show four different vertices meeting at point D.

		In figure 1 there is only one possible kite with these corners. Its sides are: AB, BC, CD and DA and it is a convex polygon.
Figure 1
		In figure 2 there are three possible kites with these corners. Their sides are: Kite 1: AD, DB, BC and CA; Kite 2: AB, BC, CD and DA; Kite 3: AB, BD, DC and CA. None of them is convex.
Figure 2

		In figure 3, the diagonals, shown as dotted blue lines, are AC and BD.
Figure 3
		In figure 4, the diagonals, shown as dotted blue lines, are respectively, Kite 1: AB and CD Kite 2: AC and BD Kite 3: AD and BC.
Figure 4

	Kite ABCD
	Rotate ABCD 180° around the middle point of AB
	Rotate ABCD 180° around middle point of BC
	Rotate ABCD 180° around middle point of CD
	Rotate ABCD 180° around middle point AD.

KITES