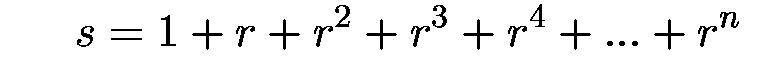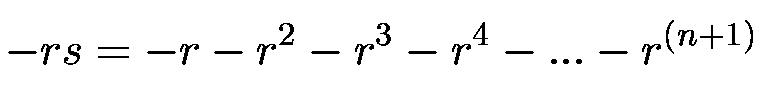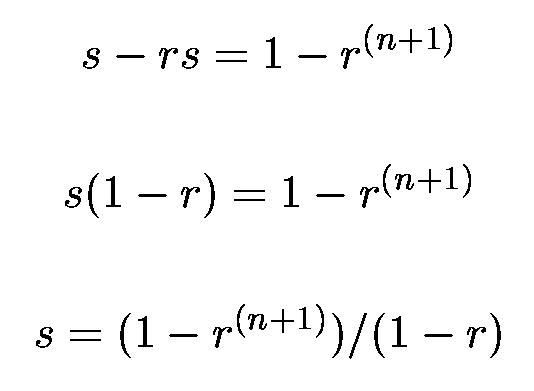
Introduction
In this lesson, you will learn how to make colorful triangles also known as Sierpinski's Carpet or Sierpinski's
Gasket, after W. Sierpinski (1882-1969). Watch a black-and-white Sierpinski's Carpet appear from
nowhere.
Activity
 Supplies: Paper, Rulers, Markers, or Crayons
Supplies: Paper, Rulers, Markers, or Crayons
Basic Instructions
- Draw an equilateral triangle with edges approximately 9 inches long.
- Connect the middle points of these edges to form a smaller central triangle with ¼ of the area. Color it green.
- In the three outlying triangles, connect the middles of the edges, creating three small triangles. Color them yellow.
- Now you have nine uncolored triangles. Again, connect the middles of their edges and create nine central triangles, which you color blue.
- Finally, create 27 small triangles in the middles of the uncolored triangles, and color them red.
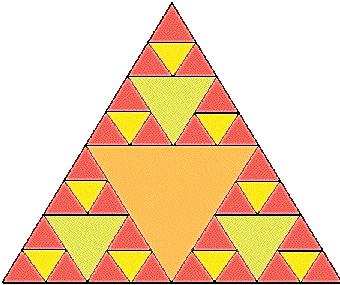
- An uncolored Sierpinski Carpet looks like this. You can print this out and have your students color the triangles.
- This Sierpinski's Carpet was made by a student.
Now stop and use your imagination. What would happen if you continued to make smaller and smaller triangles? Would you fill up the whole big triangle? What is left is smaller and smaller.
1. Let's compute the area covered by the colored triangles.
- Green takes ¼ of the total, leaving ¾ of the total.
- Yellow takes ¼ of what is left, which is ¼ of ¾, leaving ¾ * ¾ of the total area..
- Blue takes ¼ of what is left , leaving ¾ * ¾ * ¾ of the total area.
- Red takes ¼ of what is left, leaving ¾ * ¾ * ¾ * ¾ of the total area.
Thus if we would continue, we would cover
¼ + (
¼ *
¾) + (
¼ *
(¾)²) + (
¼ *
(¾)³) + ... =
¼ * (
1 +
¾ +
(¾)² +
(¾)³ + ... )
which is the sum of a geometric progression with factor ¾, multiplied by ¼.
2. The sum of this geometric progression is 1/(1 - ¾) = 4 (see below). Thus the area covered is ¼ * 4 = 1, namely,
the whole area. Thus, in the limit, we color the whole area, even if some individual points will remain uncolored.
Remark: Beginning with an equilateral triangle is done just for artistic purposes. The result holds also for any other triangle.
3. How to Sum a Geometric Progression
Let
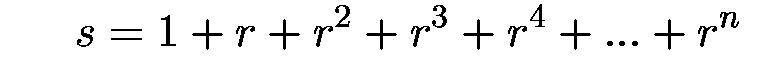
Then, multiplying by -r,
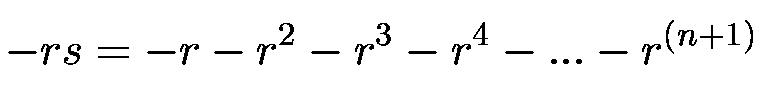
Adding the 2 equations above,
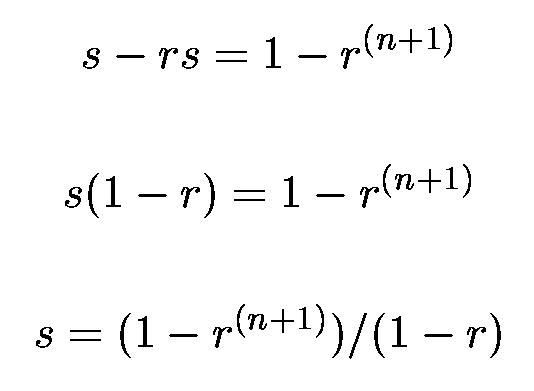
When r < 1, r n+1 approaches 0 as n gets very large. In the case above, r = ¾ so s approaches 1/(1-r).
|