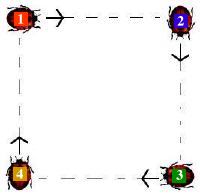
Four Bugs
Introduction
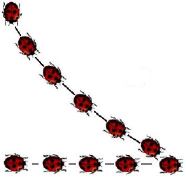
When animals chase each other, they do it in many different ways. Some try to get ahead of the one they are chasing, but others do this in a very simple way. They run full speed toward the animal they are chasing. This leads to a curved path if the other animal tries to escape sideways. Here's an example.

In the picture to the right, one ladybug starts from the top and chases the other ladybug, who tries to escape to the right. The path taken by the first ladybug is a curve.


Problem : There were four bugs standing at four corners of a square, 15 by 15 centimeters.

The bugs start chasing each other:
1 chases 2
2 chases 3
3 chases 4
4 chases 1

All bugs are running with a speed of 1 cm per second (1 cm/s). Will they catch each other? How soon? In which location?
Answer : They all meet in the center of the square after 15 seconds.

This problem can be solved in different ways in different grades.

Activity

Supplies: paper, pencils (colored pencils optional), rulers

1. Middle School and High School
By the rotational symmetry of the situation, the bugs will always be on the four corners of a square whose center remains stationary. Because a bug that is chasing always runs in a direction that is perpendicular to the direction of escape, the distance between bugs decreases by the value of their running speed, namely, by 1 cm/s. Therefore, they meet in the center after 15 seconds, each one traveling a distance of 15 cm on a spiral curving toward the center.

2. Earlier Grades
In earlier grades, the problem should be solved approximately, following the method described below.

Problems with continuous motion can be solved approximately by dividing them into steps of some constant, or changing, duration. A shorter duration for a step gives a better approximation, but it requires more work.

Let's start with 2 second steps, and later shorten the steps to 1 second, or even less.

The initial position of the bugs is shown in this picture. To see the picture in full resolution, click on the image.


Here is a larger picture which you can print out by using the PRINT function on your web browser. For two seconds, all the bugs travel straight toward the initial position of their neighbor. (Draw only short segments of straight lines. Measure the distance traveled with a ruler. Be precise.) Here is what it looks like on the picture:



The bugs turn and travel for two seconds toward the new positions of their neighbors. And so on. Watch what happens to the bugs as they keep chasing their neighbor.

When they get closer, the time intervals must get shorter. The actual path would be shorter than the one that is drawn (so the time of travel would also be shorter) because the bugs would "round the sharp corners".

Remarks
1. In early grades children should get a sheet of typing paper with the four dots marked. The actual construction of the paths the bugs take must be done precisely, with a ruler. At the end, after children have drawn the sequence of segments, they may draw the bugs, preferably at the corners of the square, and color their trajectories (the lines of movement for the bugs) with colored markers or crayons. This will provide a cohesive element between the problem (bugs chasing each other) and its solution (the paths that they take). Children may also draw and color the squares.

2. The unit has been taught in several different grades (including first and second). Often teachers have students "connect the bugs" with straight lines each time after all four bugs have moved. This creates a sequence of squares which they can color at the end. On the left is a drawing from a second grader and on the right is one made by an undergraduate student teacher. (Click on the pictures to see them larger.)

3. This is a very powerful method. In its analytic (and not graphic) form it is a basis for solving systems of differential equations.

4. The method generalizes to any number of bugs. To the right is a picture created when six bugs chased each other beginning from the corners of a regular hexagon. Bugs may travel with different speeds and start from any configuration. But the analytic solution in such a case is beyond school mathematics.

Webpage Maintained by Owen Ramsey
Lesson Index