This lesson has two versions. One is for higher grades and uses the TI-34 II calculator. The other one is for early grades and uses a four-operation calculator, the TI-108. The part that is common to both lessons is that students design, cut out from construction paper, and display a collection of regular polygons.
Task for higher grades.
Design, cut out from colored construction paper, and display in the classroom a collection of regular polygons.All the polygons must have the same area.The suggested area is A = 20 square inches, but other values are possible, and their choice may depend on the supplies that are available.1. Analysis of the problem.
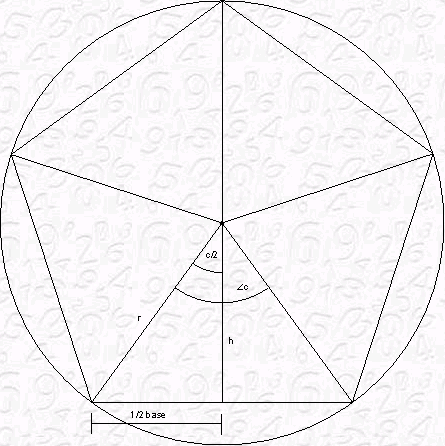
It is not difficult to construct a regular n-gon inscribed in a circle of radius r.We only need to compute the "central" angle c = 360°/n, and use a protractor to divide the circle into n equal angles of size c°. In the picture below, c = 360°/5 = 72°.We need to solve this equation for r. So we have
r = √(A/(n*cos(180/n)*sin(180/n)).
2. Computation of r.
Variables:
>A : keeps the area (here 20 square inches)
B : keeps the radius r
Ans : stores the current display, which is the number of sides n.
Define:
OP1 = √(A/(Ans*cos(180/Ans)*sin(180/Ans))→B
This gives us r.
Since our ruler measures in 32nds of an inch, we want to change the measurement to some whole number of inches plus some number of 32nds of an inch.So we also defineOP2= round(fPart(Ans)*32,1)
(This will tell how many 32nds of an inch we need.)
Set [2nd][DR] to DEG (angles are measured in degrees).
Enter 20→A
Now, in order to compute r in inches, execute, for n = 3, 4, 5, ...
n [=]
OP1 computes r, displays it, and also stores it in B. Write down the whole part.OP2 computes the number of32nds of an inch.
Here is a table of values:
|
n=no. of sides in regular polygon |
radius r of circle whose inscribed regular polygon with n sides has area 20 square inches |
radius r in inches and 32nds of an inch |
|
3 |
3.923774609 inches |
3 29.6/32 inches |
|
4 |
3.16227766 |
3 3.2/32 |
|
5 |
2.900292708 |
3 28.8/32 |
|
6 |
2.774527634 |
2 24.8/32 |
|
7 |
2.703487703 |
2 22.5/32 |
|
8 |
2.659147948 |
2 21.1/32 |
|
9 |
2.629511004 |
2 20.1/32 |


A task for lower grades.
Students compute the "central" angle mentally or with a TI-108 calculator, draw a circle of any size, and then craw and cut out the inscribed polygon. Dividing a circle into equal sectors using a protractor is a challenging task, which is the center of this activity.
Last Modified: March 12, 2007