Inscribed Triangle

(with two proofs at end)

 

This lesson can be taught in early grades. The only tools needed are scissors, protractors and rulers (with centimeters and millimeters). Children should already know that the sum of the angles of a triangle is 180°.

The lesson can also be extended to a middle or high school lesson, involving a little trigonometry (see last part).

 

Materials.

Each child is given a square piece of rather stiff paper or a piece of nicely colored origami paper, scissors, a protractor, and a ruler.

 

Task 1.

Find out what the biggest equilateral triangle is which can be cut out of a square piece of paper. Cut it out carefully. Save the remaining pieces. Precision counts!

 

Solution.

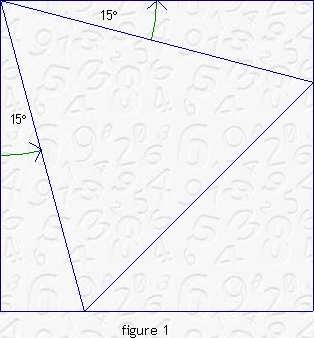
The unique solution is given in figure 1. Children can compare it to other proposals, but a proof that this configuration gives the biggest equilateral triangle inscribed in a square should not be required. Drawing the triangle starts with drawing 15° angles in one corner of the square piece of paper. This is tricky to do precisely. Therefore children should carefully measure all three edges of the triangle to check that they are the same length, before they start cutting.

Question.

Is the area of the equilateral triangle bigger than, equal to, or smaller than, half of the area of the original square?

 

Task 2.

Cut the corners (the two small isosceles right triangles) from the two smaller remaining pieces, as shown in figure 2. (The teacher should show how to do it.) Now we have 5 pieces left (besides the equilateral triangle): one big right triangle, two very small isosceles right triangles, and two medium size (obtuse) triangles.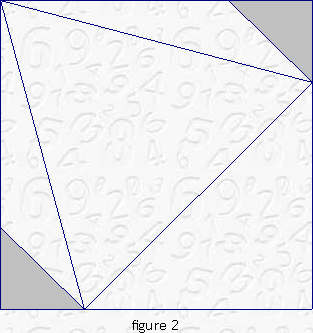

 

Task 3.

Arrange the big right triangle and the two middle size (obtuse) triangles into an equilateral triangle. (See figure 3.)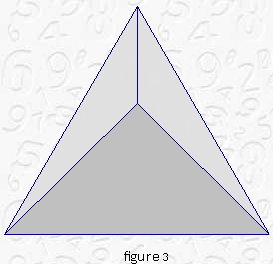

 

Answer to the question.

Notice that the assembled and cut out equilateral triangles are congruent. Thus the area of the equilateral triangle is less than half of the area of the square. Two small isosceles right triangles are the difference. Now each child has a six-piece puzzle.

 

Task 4.

Reassemble the pieces to form the square again. (See fig 4.) Make other interesting shapes.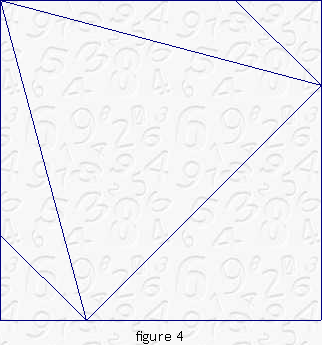

 

Extending the lesson to middle or high school, with a little trigonometry.

Task 5.

What is the area of the two tall skinny right triangles in figure 1, as a function of the length of the edge of the square, s? (This requires the use of a calculator with trigonometric functions. We used the TI-34 II.)

 

Their two areas sum to s2*tan(15°). (Do you see it?)

 

What is the area of the equilateral triangle?

 

The area of the equilateral triangle as a fraction of the area of the square is,

      (s2 - s2*(tan(15)2)/s2)/2 = (1 - (tan(15))2)/2

(This is derived step-by-step in the two proofs below.)

 

To evaluate the expression (1 - (tan(15))2)/2, use the TI-34 II. Be sure it is set on degrees and not radians.

(1-tan(15)^2)2 [=] .464101615 (46.5%)

 

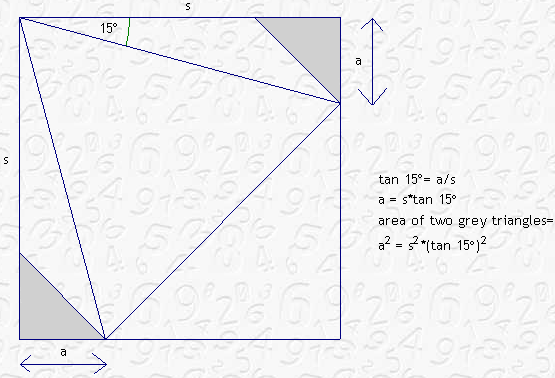
Let's look again at the area of the equilateral triangle as a fraction of the area of the square.

 

 

First proof.

Assume we know that the area of the equilateral triangle is equal to one half of the area of the white part in the diagram above. With this assumption, the proof is shorter.

First, each small grey triangle has area s2*(tan 15°)2/2. Do you see it? So the area of them both is s2*(tan 15°)2.

The area of the white part is the area of the square minus the area of the two small gray triangles, namely, s2 - s2(tan 15°)2 = s2(1- (tan 15°)2)

Dividing this by 2, we have the area of the equilateral triangle: s2(1- (tan 15°)2)/2.

Finally, we form the ratio of the area of the triangle to the area of the square:

(s2(1- (tan 15°)2)/2)/s2.

Simplifying,

Area of triangle/area of square = (1- (tan 15°)2)/2) = .464101615 (46.5%)

 

Second proof.

Assume we do not know the area of the equilateral triangle as a function of the area of the square. This makes the proof more difficult. We will find the areas of the two long skinny right triangles and the big isosceles right triangle, and subtract these two areas from the area of the whole square, leaving the area of the equilateral triangle. We will then form the ratio of the area of the triangle to the area of the square.

 

1. area of long skinny triangle = 1/2*b*h= 1/2*s*s*tan 15°

area of 2 long skinny triangles = 2*(1/2*s*s*tan 15°) = s2*tan 15°

 

2. area of large isosceles right triangle = 1/2*b*h

b = h = s - s*tan 15°, so

area of isosceles right triangle = 1/2*(s - s*tan 15°)2 = 1/2*(s2-2s2tan 15° + s2(tan 15°)2)

 

3. area of equilateral triangle = area of square - area of 2 long skinny right triangles - area of isosceles right triangle

= s2 - s2*tan 15° - 1/2*(s2-2s2tan 15° + s2(tan 15°)2)

= s2 - s2*tan 15° - s2/2 + s2tan 15° - s2/2*(tan 15°)2

Simplifying,

= s2/2 - s2/2*(tan 15°)2 = s2/2*(1 - (tan 15°)2)

Do you see that this last expression shows that the area of the equilateral triangle is a little less than 1/2 times the area of the square?

 

4. ratio of area of equilateral triangle to area of square

= [s2/2*(1 - (tan 15°)2)]/s2

= (1 - (tan 15°)2)/2 ≈ 0.464 ≈ 46%.

 

Do you see the difference between the two proofs? Proof 1 assumes we know that the area of the equilateral triangle is one half of the white area in the figure above. Proof 2 does not make this assumption.

 

Webpage Maintained by Owen Ramsey
Lesson Index