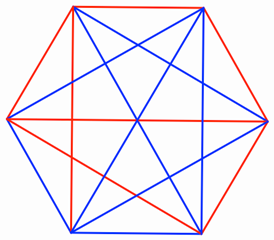
Coloring lines in a hexagon
When you
draw a regular hexagon with all diagonals, you draw 15 segments, 6 sides, 6
short diagonals, and three long diagonals. Draw these segments with two colors,
for example red and blue. Did you draw a blue triangle or a red triangle? (A
triangle is blue if all its sides are blue.)
I bet
you that you did! I even bet you that you drew at least two monochromatic (of
one color) triangles, two blue, two red or one red and one blue. (The two triangles
do not have to be disjoint; they may have one side in common.)
Can you
prove it?
--------------------------------------------------------------------------
It is
easy to prove that there is at least one triangle of the same color.
Each
vertex A is connected by segments with 5 others so at least three segments have
the same color (let’s
say blue).
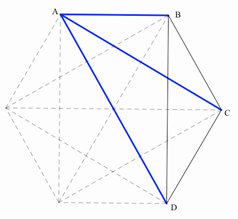
If any
of the three segments between B, C, and D is also blue, we have a blue
triangle. But if all three of them are red, we have a red triangle. (Do you see
it?)
To prove
that we always have a second triangle is a little more complex because it
requires looking at several case (a proof is given below).
There is
another possible approach. We can look at all possible colorings of lines in a
hexagon with 2 colors, and to check that in each case we have at least two
monochromatic triangles. There are only 15 lines. So there are only 215
(≈ 32,000) cases to look at. Before computers
were invented the task was prohibitively complex. But now anybody having
reasonable programming skills could use this technique.
Remark.
Don't avoid the word "monochromatic". Mono- means one, and -chromatic means colored. "Ch" in chromatic is pronounced "k".
Here is
a more elegant proof that there are at least two monochromatic triangles.
An angle
consists of two segments with a common vertex. It is monochromatic if both
segments have the same color.
We are
going to count the number M of monochromatic triangles in two ways, and compare
the results.
(1) At each
vertex we have at least 4 monochromatic angles, because
if all 5 edges are of the same color we have 10 such angles (can you count them?);
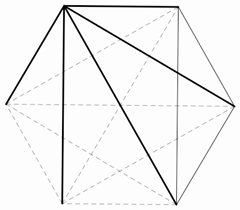
if 4 edges have one color and 1 the
other color, we have 6 such angles;
if 3 edges have one color and 2 the
other color, we have 4 such angles.
So,
because there are 6 vertices, we have,
M ≥ 6*4 = 24
(2)
There are (6 C 3) = 20 triangles in the hexagon. Let x be the number of monochromatic
triangles. The remaining 20 - x are not monochromatic.
Each monochromatic triangle has 3
monochromatic angles;
each not monochromatic triangle has
1 monochromatic angle.
So, the
number of monochromatic angles is
M = x*3 + (20 - x)*1 =
2*x + 20
Substituting
this value to previous inequality yields,
2*x + 20 ≥ 24,
and
therefore x ≥2.
So there
are at least 2 monochromatic triangles in the hexagon.