Chords in a circle
A chord in a circle is a straight line segment from one point on the border of the circle to another point.
Draw a circle. Pick (randomly from a uniform distribution) two points on the border of the circle and form a chord.
Question: What is the probability that the chord is longer than one radius?
Here is an example:
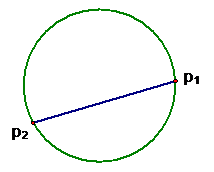
One way to investigate this problem:
1. Draw a circle with radius r of your choice.
2. Randomly choose an angle A between 0 and 360°, with vertex at the center of your circle. You may use a TI-83/84 (or a TI-34): 360*rand→A.
3. The angle defines a point on the circumference of the circle, (rcos(A), rsin(A)). (Do you see this?)
4. To get the second point, get another angle: 360*rand→B. The second point is (rcos(B), rsin (B)).
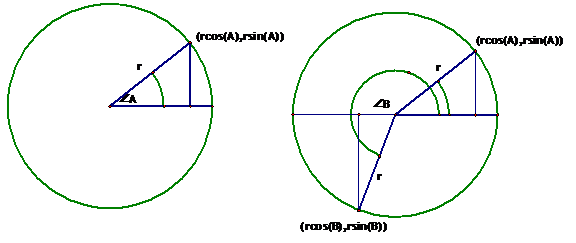
5. To find the distance between the two points, use the Pythagorean theorem:
distance = √ ((rcos(A) - rcos (B))2 + (rsin(A) - rsin(B))2).

We want to know the probability that this distance is greater than the length of the radius.
You can investigate the question using a program on the TI-83/84. The program below draws a circle, generates pairs of points on the circumference of the circle, plots and displays the segments between them, computes their lengths, and computes the percentage of segments that are greater than or equal to one radius in length. On each trial, you will see the new segment drawn in the circle. When you stop the program, the number of segments drawn (the number of trials) will be stored in N, and the percentages of segments with lengths less than and greater than the radius are stored in L2.
PROGRAM:CHORD
| :Degree | The angles are to be measured in degrees. |
| :{0,0}→L1 | Make a list with two elements, both equal to 0. |
| :ZStandard | The graphing window varies from x = -15 to +15, y = -10 to +10. |
| :ClrDraw | Clear any drawing in the graphing window. |
| :10→R | Set the radius of a circle to 10, and draw a |
| :Circle (0,0,R) | circle. It fits nicely on the screen. |
| :While 1 | Start a loop until it is interrupted by the user. |
| :360*rand→A | Randomly generate angles A and B between 0 and 360 |
| :360*rand→B | degrees. |
| :√((Rcos(A)-Rcos(B))2 -(Rsin(A)-Rsin(B))2)>R→C | Compute the distance between corresponding points on the circumference of the circle. |
| :Disp C | Display C = 0 if ≤R and C = 1 if > R. |
| :Pause | |
| :Line(Rcos(A),Rsin(A),Rcos(B),Rsin(B)) | Draw a segment between the two points. |
| :1+L1(C+1) →L1(C+1) | If C = 0, add 1 to the first element of list L1. It holds the number of segments ≤R. |
| If C = 1, add 1 to the second element of list L1. It holds the number of segments > R. | |
| :L1(1)+L1(2) →N | N holds the number of trials. |
| round(L1/N*100,1) →L2 | List L2 holds 2 things, the percentages of trials ≤ R and > R. |
| :Pause | |
| :End |
Here is a sequence of zeroes and ones, values for C above, from the program. 0 means the segment generated has length less than one radius, and 1 means it has length greater than one radius.

A circle with segments drawn in it:

I stopped the program after 36 trials, and here are my results:

So in my sample, 27.8% of my lines had lengths less than or equal to the radius, and 72.2% had lengths greater than the radius.
Proof that the probability that pairs of points are greater than one radius apart is 2/3:
Take a point P on the circumference of the circle. Measure one radius, and swing an arc from P cutting the circle on either side of P. Call these points Q and R. Continue in this fashion and you will have the 6 vertices of a regular hexagon equally spaced around the circle's circumference.
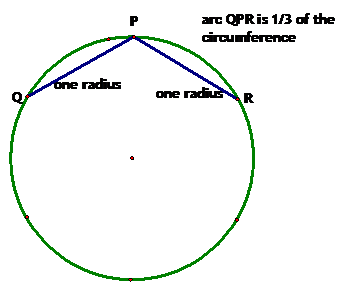
Any point lying on arc QPR is less than or equal to one radius away from P. The arc is 1/3 the border of the circle. Any point lying on the other part of the border, which is 2/3 of the circumference, is greater than or equal to one radius away from P.
So the probability is 2/3 that two points on the border are greater than or equal to one radius apart!