Cutting a triangle into two pieces of equal area and equal perimeter
Suppose you are given an arbitrary triangle (see the figure). Can you cut it with one straight line into two parts such that the two have equal area and equal perimeter?
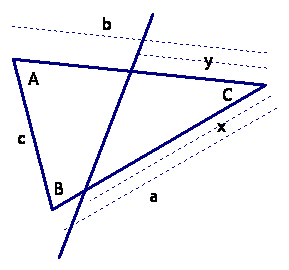
If there is a solution to the problem, then a dividing line separates the triangle into a smaller triangle and a quadrilateral (see the picture above). We name the sides of the large triangle a, b, and c, and the angles A, B, and C, as shown in the figure. These are constants because they are known values. We label the lengths of the two edges of the smaller triangle x and y. They are variables whose values are to be found.
If there is a solution, then the triangle and the quadrilateral have the same perimeter, so:
x + y = (a-x) + (b-y) + c
= a - x + b - y + c
2*(x + y) = a + b + c
x + y = (a + b + c)/2 (half the perimeter)
What we know about the (small) triangle:
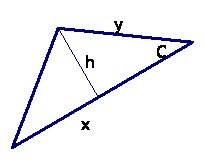
We draw height h. Let S be the area of the small triangle. Then
S = 1/2* x*h
sin C = h/y
h = y*sin C
S = 1/2*x*y*sin C
Let T be the area of the original whole triangle.
T = 1/2 *a*b*sin C
If there is a solution to the problem, then S = 1/2*T, so
1/2*a*b*sin C = x*y*sin C
1/2*a*b = x*y
So:
x*y = 1/2*a*b
And from above we know that x + y = (a + b + c)/2.
The constraints on x and y are that
a > x > 0, and b > y > 0.
Here is a trick:
We define a new variable t that can be equal to either x or y. Then
(t - x)*(t - y) = 0
(t - x)*(t - y) = t2 - x*t - y*t + x*y
(t - x)*(t - y) = t2 - (x + y)*t + x*y
From the above equations involving x*y and x + y, we have
(t - x)*(t - y) = t2 - ((a + b + c)/2)*t + 1/2*a*b = 0 (1)
If we can solve this equation, its two solutions give us x and y, provided the constraints above are satisfied.
We can write (1) as
t2 - E*t + F = 0, where E=(a + b + c)/2 and F = 1/2*a*b (2)
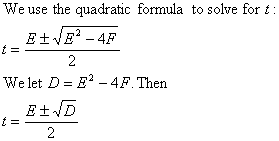
Equation (2) has solutions if D >= 0, and they are:
x = (E - √D)/ 2 (the smaller solution), and
x = (E + √D)/2 (the bigger solution).
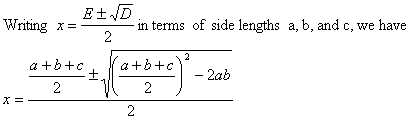
Finding solutions for a triangle whose sides have lengths 3, 4, and 5 units.
There are 3! = 6 possible solutions. But since a and b are not distinguishable in formula (1) above, there are only 3 possible solutions. They are:
(i) a = 3, b = 4, c = 5.
(ii) a = 4, b = 5, c = 3.
(iii) a = 3, b = 5, c = 4.
(i) a = 3, b = 4, c = 5.
x = (6 - √12)/2 = 1.27; y = (6 + √12)/2 = 4.73.
But the constraints are that a > x > 0, and b > y > 0.
These are not solutions to the problem because, while a = 3 > x = 1.27, it is not the case that b = 4 > y = 4.73.
(ii) a = 4, b = 5, c = 3.
x = (6 - √6)/2 = 1.78; y = (6 + √6)/2 = 4.22.
These are solutions to the problem, because a = 4 > x = 1.78, and b = 5 > 4.22.
(iii) a = 3, b = 5, c = 4.
Here D = E2 - 4*F = -4 < 0, so the equation has no solution.
So there is only one solution, x and y, to the problem: x = 1.78 and y = 4.22.
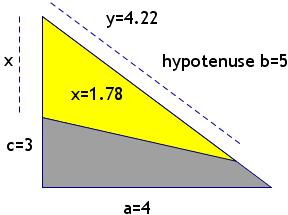
The yellow triangle and grey quadrilateral have the same area and the same perimeter. Do you know how to check it?